【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
参考答案:
【答案】(1)一个足球的单价103元,一个篮球的单价56元;(2)9.
【解析】试题分析:(1)设一个足球的单价x元、一个篮球的单价为y元,根据:①1个足球费用+1个篮球费用=159元,②足球单价是篮球单价的2倍少9元,据此列方程组求解即可;
(2)设买足球m个,则买蓝球(20﹣m)个,根据购买足球和篮球的总费用不超过1550元建立不等式求出其解即可.
试题解析:(1)设一个足球的单价x元、一个篮球的单价为y元,根据题意得: ![]() ,解得:
,解得: ![]() .
.
答:一个足球的单价103元,一个篮球的单价56元;
(2)设可买足球m个,则买蓝球(20﹣m)个,根据题意得:
103m+56(20﹣m)≤1550,解得:m≤![]() ,∵m为整数,∴m最大取9
,∵m为整数,∴m最大取9
答:学校最多可以买9个足球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数0.397精确到0.01的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “整体思想”是中学数学解题中一种重要的思想方法,它在多项式的化简与求值中应用极为广泛.如:已知m+n=﹣2,mn=﹣4,则2(mn﹣3m)﹣3(2n﹣mn)的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,下列哪个点与△ABC的任意两个顶点,围成的三角形都是等腰三角形( )
A.三条中线的交点
B.三条高线的交点
C.三条角平分线的交点
D.三条垂直平分线的交点 -
科目: 来源: 题型:
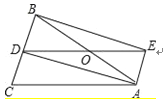
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为促销,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元;打折后,买50件A商品和40件B商品仅需364元,这比打折前少花多少钱?
-
科目: 来源: 题型:
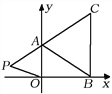
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
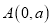 ,
, 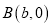 ,
, 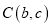 三点,其中
三点,其中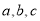 满足关系式
满足关系式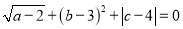 .
.
(1)求
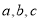 的值;
的值; (2)如果在第二象限内有一点
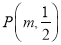 ,那么请用含
,那么请用含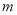 的式子表示四边形
的式子表示四边形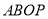 的面积;
的面积;(3)在(2)的条件下,是否存在点
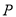 ,使四边形
,使四边形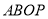 的面积与三角形
的面积与三角形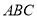 的面积相等?若存在,求出点
的面积相等?若存在,求出点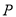 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

