【题目】如图1,已知![]() 的边
的边![]() 平行于
平行于![]() 轴,
轴,![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第四象限,点
在第四象限,点![]() 是
是![]() 边上的一个动点.
边上的一个动点.

(1)若点![]() 在边
在边![]() 上,
上,![]() 求点
求点![]() 的坐标;
的坐标;
(2)若点![]() 在边
在边![]() 或
或![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点如图2,过点
轴的交点如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 过点
过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 它们相交于点
它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)
参考答案:
【答案】(1) (3,4); (2) (![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
(1)由题意点P与点C重合,可得点P坐标为(3,4);
(2)分类讨论,①当点P在线段CD上时,②当点P在线段AD上时,分别求解即可.
(1)∵CD=6,点P在边BC上,
∴点P与点C重合,
∵AB平行于![]() 轴,
轴,![]() ,且四边形ABCD是平行四边形,
,且四边形ABCD是平行四边形,
∴CD∥AB∥![]() 轴,则点C的纵坐标与点D的纵坐标相同,
轴,则点C的纵坐标与点D的纵坐标相同,
∴点C坐标为(3,4),
∴点P坐标为(3,4);
(2)∵点A、D的坐标分别为(1,-4),(-3,4);
设直线AD的解析式为![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∵直线AD的解析式为![]() ,
,
令![]() ,则
,则![]() ,
,
∴点G坐标为(0,![]() );
);
①如图中,当点P在线段CD上时,设P(![]() ,4).
,4).
根据折叠的性质,PM′= PM=4+2=6,ON=GM=G M′=m,
在Rt△PNM′中,∵PM′= PM=4+2=6,PN=4,
∴NM′=![]() ,
,
在Rt△OGM′中,![]() NM′-ON=
NM′-ON=![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,
∴点P坐标为(![]() ,
,![]() ),
),
根据对称性可知,P(![]() ,
,![]() )也满足条件;
)也满足条件;
②如图中,当点P在线段AD上时,设AD交![]() 轴于R.
轴于R.

根据折叠的性质,∠MGP=∠M′GP,M′G=GM,
又MG∥![]() 轴,
轴,
∴∠MGP=∠M′RG,
∴∠M′RG=∠M′GR,
∴M′R=M′G=GM,
设M′R=M′G=GM=![]() ,
,
∵直线AD的解析式为![]() ,
,
∴R(![]() ,0),
,0),
在Rt△OGM′中,![]() RM′-RO=
RM′-RO=![]() ,
,
∵![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴点P的横坐标为![]() ,代入直线AD的解析式
,代入直线AD的解析式![]() ,
,
得:![]() ,
,
∴点P坐标为(![]() ,
,![]() ),
),
综上,满足条件的点P坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的推理.
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,试说明:AB∥CD.
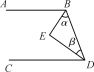
完成推理过程:
∵BE平分∠ABD(已知),
∴∠ABD=2∠α(__________).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (__________).
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)( __________).
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°(__________).
∴AB∥CD(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y1=a(x+2)2﹣3与y2=
 (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )

A. ①② B. ②③ C. ③④ D. ①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(
 ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是_____.
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, .点
.点 是射线
是射线 上一动点,过点
上一动点,过点 作射线
作射线 的垂线,垂足为点
的垂线,垂足为点 ,点
,点 为
为 的中点,连结
的中点,连结 ,则
,则 的最小值为________.
的最小值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在读书月活动中,学校准备购买一批课外读物.为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根
据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,艺术类读物所在扇形的圆心角是 度;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校购买其他类读物多少册比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…第n次移动到An.则△OA6A2020的面积是( )
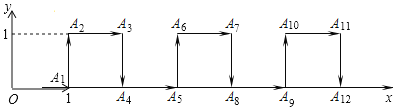
A.505
 B.504.5
B.504.5 C.505.5
C.505.5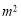 D.1010
D.1010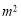
相关试题

