【题目】某次水灾导致大约有![]() 人无家可归,假如一顶帐篷占地
人无家可归,假如一顶帐篷占地![]() ,可以放置40个单人床位.
,可以放置40个单人床位.
(1)为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多大地方?
(2)若学校的操场面积为![]() ,可安置多少人?
,可安置多少人?
(3)要安置所有无家可归的人,大约需要多少个这样的操场?
参考答案:
【答案】(1)这些帐篷大约要占![]() ;(2)可安置
;(2)可安置![]() 人;(3)大约需要操场90个.
人;(3)大约需要操场90个.
【解析】
(1)帐篷总数=总人数÷每张帐篷安置的人数,帐篷总占地面积=一顶帐篷的面积×帐篷总数;
(2)学校的操场安置的人数=操场面积÷一顶帐篷的面积×每张帐篷安置的人数;
(3)操场个数=无家可归的总人数÷一个操场安置的人数.
解:(1)需要帐篷![]() (顶)
(顶)
这些帐篷大约要占![]() ;
;
(2)可安置![]() (人)
(人)
(3)大约需要操场![]() (个)
(个)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系,F是BC边上的点,过F点的反比例函数y=
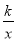 (k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
(k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.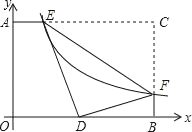
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
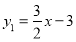 的图象与反比例函数
的图象与反比例函数 第一象限内的图象相交于点
第一象限内的图象相交于点 ,与
,与 轴相交于点
轴相交于点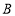 .
.(1)求
 和
和 的值;
的值;(2)观察反比例函数
 的图象,当
的图象,当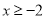 时,请直接写出
时,请直接写出 的取值范围;
的取值范围;(3)如图,以
 为边作菱形
为边作菱形 ,使点
,使点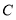 在
在 轴正半轴上,点
轴正半轴上,点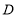 在第一象限,双曲线交
在第一象限,双曲线交 于点
于点 ,连接
,连接 、
、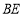 ,求
,求 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
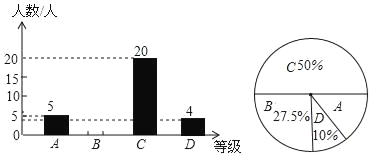
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=
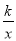 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B是线段AC上一点,AC=4AB,AB=6cm,直线MN经过线段BC的中点P.
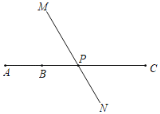
(1)图中共有线段_____条,图中共有射线_____条.
(2)图中与∠MPC互补的角是_____.
(3)线段AP的长度是_____.
相关试题

