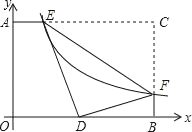
【题目】如图,在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系,F是BC边上的点,过F点的反比例函数y=![]() (k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
(k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
参考答案:
【答案】(4, ![]() ).
).
【解析】过点E作ED⊥OB于点D,根据折叠的性质得∠EMF=∠C=90°,EC=EM,CF=DF,易证Rt△MEM∽Rt△BMF;而EC=AC-AE=4-![]() ,CF=BC-BF=3-
,CF=BC-BF=3-![]() ,得到EM=4-
,得到EM=4-![]() ,MF=3-
,MF=3-![]() ,即可得
,即可得![]() ;故可得出EM:MB=ED:MF=4:3,而ED=3,从而求出BM=
;故可得出EM:MB=ED:MF=4:3,而ED=3,从而求出BM=![]() ,然后在Rt△MBF中利用勾股定理得到关于k的方程(3-
,然后在Rt△MBF中利用勾股定理得到关于k的方程(3-![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,解方程求出k=
)2,解方程求出k=![]() ,即可得解析式y=
,即可得解析式y=![]() ,代入x=4得到F点的坐标(4,
,代入x=4得到F点的坐标(4, ![]() ).
).
故答案为:(4, ![]() ).
).
-
科目: 来源: 题型:
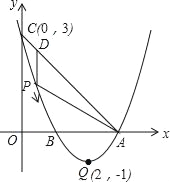
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.
(1)求该抛物线的函数关系式;
(2)当△ADP是直角三角形时,求点P的坐标;
(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一组数据x1 , x2 , x3 , x4 , x5 , x6的平均数是2,方差是2,则另一组数据3x1-2 , 3x2-2 , 3x3-2 , 3x4-2 , 3x5-2 , 3x6-2的平均数和方差分别是( ).
A.2, 2 B.2, 18 C.4, 6 D.4, 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
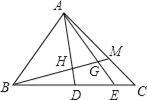
A. 3:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数
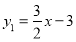 的图象与反比例函数
的图象与反比例函数 第一象限内的图象相交于点
第一象限内的图象相交于点 ,与
,与 轴相交于点
轴相交于点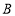 .
.(1)求
 和
和 的值;
的值;(2)观察反比例函数
 的图象,当
的图象,当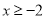 时,请直接写出
时,请直接写出 的取值范围;
的取值范围;(3)如图,以
 为边作菱形
为边作菱形 ,使点
,使点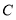 在
在 轴正半轴上,点
轴正半轴上,点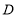 在第一象限,双曲线交
在第一象限,双曲线交 于点
于点 ,连接
,连接 、
、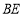 ,求
,求 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某次水灾导致大约有
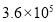 人无家可归,假如一顶帐篷占地
人无家可归,假如一顶帐篷占地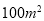 ,可以放置40个单人床位.
,可以放置40个单人床位.(1)为了安置所有无家可归的人,需要多少顶帐篷?这些帐篷大约要占多大地方?
(2)若学校的操场面积为
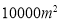 ,可安置多少人?
,可安置多少人?(3)要安置所有无家可归的人,大约需要多少个这样的操场?
相关试题

