【题目】如图1,某学校开展“交通安全日”活动.在活动中,交警叔叔向同学们展示了大货车盲区的分布情况,并提醒大家:坐在驾驶室的司机根本看不到在盲区中的同学们,所以一定要远离大货车的盲区,保护自身安全.小刚所在的学习小组为了更好的分析大货车盲区的问题,将图1用平面图形进行表示,并标注了测量出的数据,如图2.在图2中大货车的形状为矩形,而盲区1为梯形,盲区2、盲区3为直角三角形,盲区4为正方形.
请你帮助小刚的学习小组解决下面的问题:
(1)盲区1的面积约是多少m2;盲区2的面积约是多少m2;
(![]() ≈1.4,
≈1.4,![]() ≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
≈1.7,sin25°≈0.4,cos25°≈0.9,tan25°≈05,结果保留整数)
(2)如果以大货车的中心A点为圆心,覆盖所有盲区的半径最小的圆为大货车的危险区域,请在图2中画出大货车的危险区域.
参考答案:
【答案】(1)盲区1的面积约是5m2;盲区2的面积约是4m2;(2)以A为圆心,AC长为半径所画的圆为大货车的危险区域.如图所示见解析.
【解析】
(1)作OP⊥CD于P.根据等腰梯形的性质求出DP=![]() (CD﹣OB)=1.解直角△ODP,得出OP=DPtan∠D=
(CD﹣OB)=1.解直角△ODP,得出OP=DPtan∠D=![]() ,再利用梯形的面积公式即可求出盲区1的面积;解直角△BEN,求出BE=
,再利用梯形的面积公式即可求出盲区1的面积;解直角△BEN,求出BE=![]() ≈4,那么S△BEN=
≈4,那么S△BEN=![]() BEEN≈4m2,即为盲区2的面积;
BEEN≈4m2,即为盲区2的面积;
(2)利用勾股定理求出AC=AD=![]() =
=![]() ,AH=AG=
,AH=AG=![]() =
=![]() ,AM=AN=
,AM=AN=![]() =
=![]() ,得到AC最大,那么以A为圆心,AC长为半径所画的圆为大货车的危险区域.
,得到AC最大,那么以A为圆心,AC长为半径所画的圆为大货车的危险区域.
(1)如图,作OP⊥CD于P.
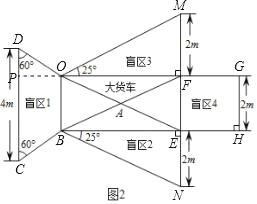
∵OBCD是等腰梯形,OB=2,CD=4,
∴DP=![]() (CD﹣OB)=1.
(CD﹣OB)=1.
在直角△ODP中,∵∠D=60°,
∴OP=DPtan∠D=1×![]() =
=![]() ,
,
∴S梯形OBCD=![]() (OB+CD)OP=
(OB+CD)OP=![]() (2+4)
(2+4)![]() =3
=3![]() ≈3×1.7≈5(m2),
≈3×1.7≈5(m2),
即盲区1的面积约是5m2;
在直角△BEN中,∵∠EBN=25°,EN=2,
∴BE=![]() =4,
=4,
∴S△BEN=![]() BEEN≈
BEEN≈![]() ×4×2=4(m2),
×4×2=4(m2),
即盲区2的面积约是4m2.
故答案为5,4;
(2)∵AC=AD=![]() ,
,
AH=AG=![]() ,
,
AM=AN=![]() ,
,
∴AC=AD>AH=AG>AM=AN,
∴以A为圆心,AC长为半径所画的圆为大货车的危险区域.
如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
在数学课上,老师请同学们思考如下问题:
请利用直尺和圆规四等分弧AB.
小亮的作法如下:
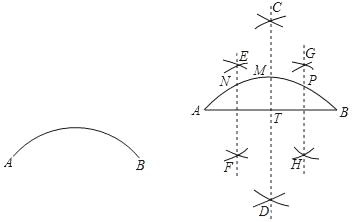
如图,
(1)连接AB;
(2)作AB的垂直平分线CD交弧AB于点M.交AB于点T;
(3)分别作线段AT,线段BT的垂直平分线EF,GH,交弧AB于N,P两点;
那么N,M,P三点把弧AB四等分.
老师问:“小亮的作法正确吗?”
请回备:小亮的作法_____(“正确”或“不正确”)理由是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=mx2﹣2mx﹣3m是二次函数.
(1)如果该二次函数的图象与y轴的交点为(0,3),求m的值;
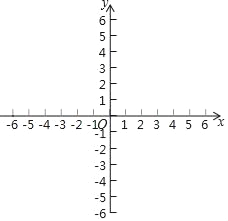
(2)在给定的坐标系中画出(1)中二次函数的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点O为正方形ABCD对角线的交点,且正方形ABCD的边均与某条坐标轴平行或垂直,AB=4.
(1)如果反比例函数y=
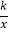 的图象经过点A,求这个反比例函数的表达式;
的图象经过点A,求这个反比例函数的表达式;(2)如果反比例函数y=
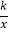 的图象与正方形ABCD有公共点,请直接写出k的取值范围.
的图象与正方形ABCD有公共点,请直接写出k的取值范围.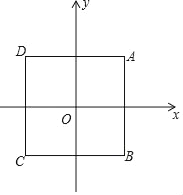
-
科目: 来源: 题型:
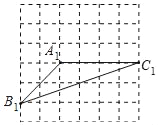
查看答案和解析>>【题目】如图是边长为1的正方形网格,△A1B1C1的顶点均在格点上.
(1)在该网格中画出△A2B2C2(顶点均在格点上),使△A2B2C2∽△A1B1C1;
(2)请写出(1)中作图的主要步骤,并说明△A2B2C2和△A1B1C1相似的依据.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,连接AC.过点B作⊙O的切线,交AC的延长线于点D,在AD上取一点E,使AE=AB,连接BE,交⊙O于点F.
请补全图形并解决下面的问题:
(1)求证:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=
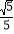 .求BD的长.
.求BD的长.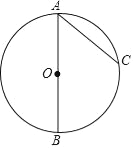
-
科目: 来源: 题型:
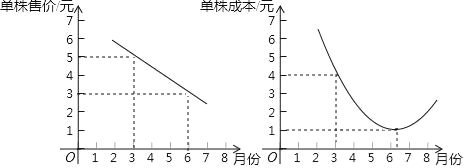
查看答案和解析>>【题目】小哲的姑妈经营一家花店,随着越来越多的人喜爱“多肉植物”,姑妈也打算销售“多肉植物”.小哲帮助姑妈针对某种“多肉植物”做了市场调查后,绘制了以下两张图表:
(1)如果在三月份出售这种植物,单株获利多少元;
(2)请你运用所学知识,帮助姑妈求出在哪个月销售这种多肉植物,单株获利最大?(提示:单株获利=单株售价﹣单株成本)
相关试题

