Question

【题目】阅读下面材料：

在数学课上，老师请同学们思考如下问题：

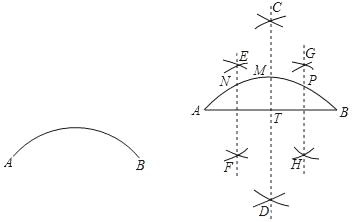
请利用直尺和圆规四等分弧AB．

小亮的作法如下：

如图，

（1）连接AB；

（2）作AB的垂直平分线CD交弧AB于点M．交AB于点T；

（3）分别作线段AT，线段BT的垂直平分线EF，GH，交弧AB于N，P两点；

那么N，M，P三点把弧AB四等分．

老师问：“小亮的作法正确吗？”

请回备：小亮的作法_____（“正确”或“不正确”）理由是_____．

Answer 1

【答案】不正确 EF，GH平分的不是弧AM，BM所对的弦

【解析】

由作法可知，弦AN与MN不相等，根据圆心角、弧、弦的关系定理得到≠，即EF平分的不是弧AM所对的弦．同理可得GH平分的不是弧BM所对的弦．由此得出小亮的作法不正确．

小亮的作法不正确．理由是：

如图，连结AN并延长，交CD于J，连结MN，设EF与AB交于I．

由作法可知，EF∥CD，AI＝IT，

∴AN＝NJ，

∵∠NMJ＞∠NJM，

∴NJ＞MN，

∴AN＞MN，

∴弦AN与MN不相等，

则≠，即EF平分的不是弧AM所对的弦．

同理可得GH平分的不是弧BM所对的弦．

故答案为不正确；EF，GH平分的不是弧AM，BM所对的弦．