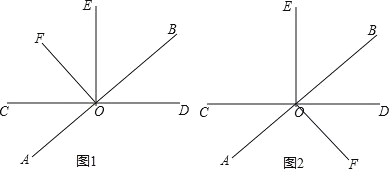
【题目】已知如图,直线![]() 相交于点
相交于点![]() .
.
(1)若∠AOC=35°,求![]() 的度数;
的度数;
(2)若∠BOD:∠BOC=2:4,求![]() 的度数;
的度数;
(3)在(2)的条件下,过点![]() 作
作![]() ,求
,求![]() 的度数.
的度数.

参考答案:
【答案】(1)55°,(2)150°,(3)60°或120°
【解析】
(1)根据AOB共线即可知![]() +
+![]() +
+![]() =180°即可解得;
=180°即可解得;
(2)根据平角的定义可求出∠BOD,根据对顶角的定义可求出∠AOC,再根据角的和差关系可求∠AOE的度数;
(3)先过点O作![]() ,再分两种情况根据角的和差关系来求∠EOF即可.
,再分两种情况根据角的和差关系来求∠EOF即可.
(1)∵∠AOC=35°,![]() ,
,
∴![]() =180°-
=180°-![]() -
-![]() =55°;-
=55°;-
(2)∵∠BOD:∠BOC=2:4,
∴![]() =180°×
=180°×![]() =60°,
=60°,
∴∠AOC=60°,
∴∠AOE=60°+90°=150°;
(3)如图1,∠EOF=150°-90°=60°,
或如图2,∠EOF=360°-150°-90°=120°,
故∠EOF的度数为60°或120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣x与反比例函数y=
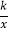 的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=
的图象交于A,B两点,过点B作BD∥x轴,交y轴于点D,直线AD交反比例函数y=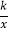 的图象于另一点C,则
的图象于另一点C,则 的值为( )
的值为( )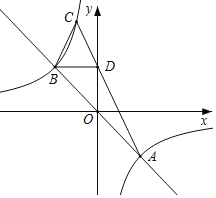
A. 1:3 B. 1:2
 C. 2:7 D. 3:10
C. 2:7 D. 3:10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1+∠4﹦180°,∠2﹦∠E,则EF∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.
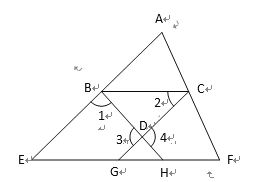
证明:
∵∠1+∠4﹦180°( ),
∠3﹦∠4 ( ),
∴∠1﹢ ﹦180°.
∴AE∥CG ( )
∴∠E﹦∠CGF( ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( ).
∴ BC∥EF( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠BAC=90°,AB=3,AC=6
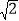 ,点D,E分别是边BC,AC上的动点,则DA+DE的最小值为_____.
,点D,E分别是边BC,AC上的动点,则DA+DE的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔C的北偏东45方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时船距灯塔的距离(参考数据:
 ≈1.414,
≈1.414,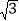 ≈1.732,结果取整数).
≈1.732,结果取整数).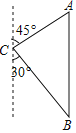
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD,CE是角平分线,则图中的等腰三角形共有
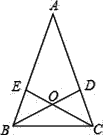
A. 8个 B. 7个 C. 6个 D. 5个
-
科目: 来源: 题型:
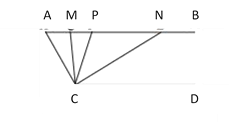
查看答案和解析>>【题目】如图,已知AB∥CD,∠A=40°,点P是射线B上一动点(与点A不重合),CM,CN分别平分∠ACP和∠PCD,分别交射线AB于点M,N.
(1)求∠MCN的度数.
(2)当点P运动到某处时,∠AMC=∠ACN,求此时∠ACM的度数.
(3)在点P运动的过程中,∠APC与∠ANC的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
相关试题

