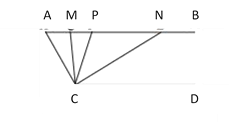
【题目】如图,已知AB∥CD,∠A=40°,点P是射线B上一动点(与点A不重合),CM,CN分别平分∠ACP和∠PCD,分别交射线AB于点M,N.
(1)求∠MCN的度数.
(2)当点P运动到某处时,∠AMC=∠ACN,求此时∠ACM的度数.
(3)在点P运动的过程中,∠APC与∠ANC的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
参考答案:
【答案】(1)∠MCN=70°;(2)∠ACM=35°;(3)不变.(详见解析)
【解析】
(1)由AB∥CD可得∠ACD=180°-∠A,再由CM、CN均为角平分线可求解;
(2)由AB∥CD可得∠AMC=∠MCD,再由∠AMC=∠ACN可得∠ACM =∠NCD;
(3)由AB∥CD可得∠APC=∠PCD,再由CN为角平分线即可解答.
解:(1)∵A B∥CD,
∴∠ACD=180°﹣∠A=140°,
又∵CM,CN分别平分∠ACP和∠PCD,
∴∠MCN=∠MCP+∠NCP=![]() (∠ACP+∠PCD)=
(∠ACP+∠PCD)=![]() ∠ACD=70°,
∠ACD=70°,
故答案为:70°.
(2)∵AB∥CD,
∴∠AMC=∠MCD,
又∵∠AMC=∠ACN,
∴∠MCD=∠ACN,
∴∠ACM=∠ACN﹣∠MCN=∠MCD﹣∠MCN=∠NCD,
∴∠ACM=∠MCP=∠NCP=∠NCD,
∴∠ACM=![]() ∠ACD=35°,
∠ACD=35°,
故答案为:35°.
(3)不变.理由如下:
∵AB∥CD,
∴∠APC=∠PCD,∠ANC=∠NCD,
又∵CN平分∠PCD,
∴∠ANC=∠NCD=![]() ∠PCD=
∠PCD=![]() ∠APC,即∠APC:∠ANC=2:1.
∠APC,即∠APC:∠ANC=2:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,直线
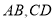 相交于点
相交于点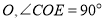 .
.(1)若∠AOC=35°,求
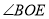 的度数;
的度数;(2)若∠BOD:∠BOC=2:4,求
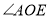 的度数;
的度数;(3)在(2)的条件下,过点
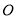 作
作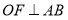 ,求
,求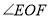 的度数.
的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔C的北偏东45方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时船距灯塔的距离(参考数据:
 ≈1.414,
≈1.414, ≈1.732,结果取整数).
≈1.732,结果取整数).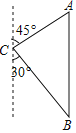
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,BD,CE是角平分线,则图中的等腰三角形共有
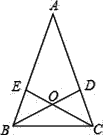
A. 8个 B. 7个 C. 6个 D. 5个
-
科目: 来源: 题型:
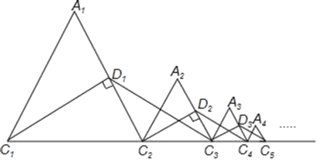
查看答案和解析>>【题目】如图,等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边△A2C2C3;作C2D2⊥A2C3于D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边△A3C3C4;…且点A1,A2,A3,…都在直线C1C2同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△AnnCn+1的周长和为_____.(n≥2,且n为整数)
-
科目: 来源: 题型:
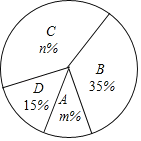
查看答案和解析>>【题目】今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级
成绩(s)
频数(人数)
A
90<s≤100
4
B
80<s≤90
x
C
70<s≤80
16
D
s≤70
6
根据以上信息,解答以下问题:
(1)表中的x= ;
(2)扇形统计图中m= ,n= ,C等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
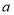 、
、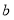 、
、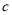 在数轴上的位置如图所示,回答下列问题:
在数轴上的位置如图所示,回答下列问题:
(1)化简:
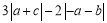 ;
; (2)令
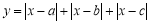 ,请问
,请问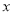 满足什么条件时,
满足什么条件时,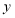 有最小值,并求出该最小值.
有最小值,并求出该最小值.
相关试题

