【题目】如图,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,且与y轴交于点C,点D是抛物线的顶点,抛物线的对称轴DE交x轴于点E,连接BD.

(1)求经过A,B,C三点的抛物线的函数表达式;
(2)点P是线段BD上一点,当PE=PC时,求点P的坐标;
(3)在(2)的条件下,过点P作PF⊥x轴于点F,G为抛物线上一动点,M为x轴上一动点,N为直线PF上一动点,当以F、M、G为顶点的四边形是正方形时,请求出点M的坐标.
参考答案:
【答案】(1)y=﹣x2+2x+3;(2)(2,2);(3)(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
试题分析:(1)利用待定系数法求出过A,B,C三点的抛物线的函数表达式;(2)连接PC、PE,利用公式求出顶点D的坐标,利用待定系数法求出直线BD的解析式,设出点P的坐标为(x,﹣2x+6),利用勾股定理表示出PC2和PE2,根据题意列出方程,解方程求出x的值,计算求出点P的坐标;(3)设点M的坐标为(a,0),表示出点G的坐标,根据正方形的性质列出方程,解方程即可.
试题解析:(1)∵抛物线y=﹣x2+bx+c经过A(﹣1,0),B(3,0)两点,
∴![]() , 解得,
, 解得,![]() , ∴经过A,B,C三点的抛物线的函数表达式为y=﹣x2+2x+3;
, ∴经过A,B,C三点的抛物线的函数表达式为y=﹣x2+2x+3;
(2)如图1,连接PC、PE, x=﹣![]() =﹣
=﹣![]() =1, 当x=1时,y=4,
=1, 当x=1时,y=4,
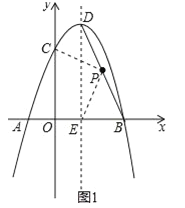
∴点D的坐标为(1,4), 设直线BD的解析式为:y=mx+n,则![]() , 解得,
, 解得,![]() ,
,
∴直线BD的解析式为y=﹣2x+6, 设点P的坐标为(x,﹣2x+6),
则PC2=x2+(3+2x﹣6)2,PE2=(x﹣1)2+(﹣2x+6)2, ∵PC=PE,
∴x2+(3+2x﹣6)2=(x﹣1)2+(﹣2x+6)2, 解得,x=2, 则y=﹣2×2+6=2, ∴点P的坐标为(2,2);
(3)设点M的坐标为(a,0),则点G的坐标为(a,﹣a2+2a+3),
∵以F、M、G为顶点的四边形是正方形, ∴FM=MG,即|2﹣a|=|﹣a2+2a+3|,
当2﹣a=﹣a2+2a+3时, 整理得,a2﹣3a﹣1=0, 解得,a=![]() ,
,
当2﹣a=﹣(﹣a2+2a+3)时, 整理得,a2﹣a﹣5=0, 解得,a=![]() ,
,
∴当以F、M、G为顶点的四边形是正方形时,点M的坐标为(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0),(
,0),(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明发现关于x的方程★x﹣6=4中的x的系数被污染了,要解方程怎么办?他翻开资料的答案一看,此方程的解为x=﹣2,则★=?( )
A.★=﹣5
B.★=3
C.★=4
D.★=﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果a+b=3,ab=2,那么代数式a2+b2的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.内错角相等B.两直线平行,同旁内角相等
C.同位角相等D.过直线外一点有且只有一条直线与已知直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以一定的速度沿同一路线行走. 设甲乙两人相距
 (米),甲行走的时间为
(米),甲行走的时间为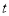 (分),
(分), 为
为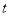 的函数,其函数图像的一部分如图所示.
的函数,其函数图像的一部分如图所示.(1)求甲、乙两人行走的速度;
(2)当甲出发多少分钟时,甲、乙两人相距390米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与
与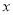 轴交于点A(-6,0),与
轴交于点A(-6,0),与 轴交于点B.
轴交于点B.(1)求b的值;
(2)把△AOB绕原点O顺时针旋转90°后,点A落在
 轴的
轴的 处,点B若在
处,点B若在 轴的
轴的 处;
处;①求直线
 的函数关系式;
的函数关系式;②设直线AB与直线
 交于点C,长方形PQMN是△
交于点C,长方形PQMN是△ 的内接长方形,其中点P,Q在线段
的内接长方形,其中点P,Q在线段 上,点M在线段
上,点M在线段 上,点N在线段AC上.若长方形PQMN的两条邻边的比为1∶2,试求长方形PQMN的周长.
上,点N在线段AC上.若长方形PQMN的两条邻边的比为1∶2,试求长方形PQMN的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
相关试题

