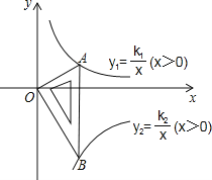
【题目】如图,一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=![]() (x>0)的图象上,∠ABO=30°,求
(x>0)的图象上,∠ABO=30°,求![]() 的值.
的值.
参考答案:
【答案】![]()
【解析】
设AC=a,则OA=2a,OC=![]() a,根据直角三角形30°角的性质和勾股定理分别计算点A和B的坐标,写出A和B两点的坐标,代入解析式求出k1和k2的值,即可求
a,根据直角三角形30°角的性质和勾股定理分别计算点A和B的坐标,写出A和B两点的坐标,代入解析式求出k1和k2的值,即可求![]() 的值.
的值.
设AB与x轴交点为点C
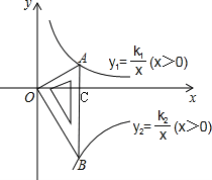
Rt△AOB中,∠B=30°,∠AOB=90°,
∴∠OAC=60°,
∵AB⊥OC,
∴∠ACO=90°,
∴∠AOC=30°,
设AC=a,则OA=2a,OC=![]() =
=![]() a,
a,
∴A(![]() a,a),
a,a),
∵A在函数y1=![]() (x>0)的图象上,
(x>0)的图象上,
∴k1=![]() a×a=
a×a=![]() a2,
a2,
Rt△BOC中,OB=2OC=2![]() a,
a,
∴BC=![]() =3a,
=3a,
∴B(![]() a,-3a),
a,-3a),
∵B在函数y2=![]() (x>0)的图象上,
(x>0)的图象上,
∴k2=-3a×![]() a=-3
a=-3![]() a2,
a2,
∴![]() =
=![]() =-
=-![]() ,
,
故答案为:-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )
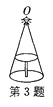
A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-
 的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
A.-1B.-2C.-3D.-4
-
科目: 来源: 题型:
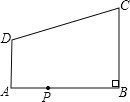
查看答案和解析>>【题目】如图,在矩形ABCD中,点E为AD上一点,且AB=8,AE=3,BC=4,点P为AB上一动点,连接PC、PE,若PAE与PBC是相似三角形,则满足条件的点P的个数有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E为ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.
(1)写出所有与△ABE相似的三角形,并选择其中一对相似三角形加以证明;
(2)若BC=2CE,求
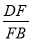 的值.
的值.
-
科目: 来源: 题型:
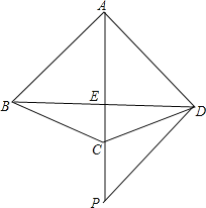
查看答案和解析>>【题目】如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
相关试题

