【题目】如图,在△ABC中,∠ABC=90°,AB∥y轴,AB=3,反比例函数y=-![]() 的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )
的图象经过点B,与AC交于点D,且CD=2AD,则点D的横坐标是( )

A.-1B.-2C.-3D.-4
参考答案:
【答案】C
【解析】
过D作AB的平行线,交BC于E,交x轴于F,得出ABEF是矩形,根据矩形的性质得出EF=AB=3.由DE∥AB,根据平行线分线段成比例定理求出DE=![]() AB=2,则DF=1,即D点纵坐标为1,再根据反比例函数y=-
AB=2,则DF=1,即D点纵坐标为1,再根据反比例函数y=-![]() 的图象经过点D,即可求出点D的横坐标.
的图象经过点D,即可求出点D的横坐标.
过D作AB的平行线,交BC于E,交x轴于F,则ABEF是矩形,EF=AB=3.
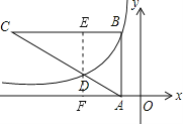
∵DE∥AB,CD=2AD,
∴![]() =
=![]() =
=![]() ,
,
∴DE=![]() AB=2,
AB=2,
∴DF=EF-DE=3-2=1,
∴D点纵坐标为1,
∵反比例函数y=-![]() 的图象经过点D,
的图象经过点D,
∴y=1时,x=-3,
∴点D的横坐标是-3.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD的各顶点坐标分别为A(1,0),B(2,0),C(2,2),D(0,1);四边形BFGH的各顶点坐标分别为F(4,0),G(4,4),H(0,2).则下列说法正确的是( )
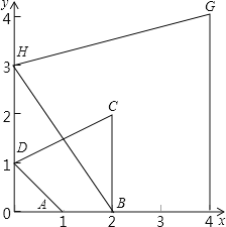
A.四边形ABCD与四边形BFGH相似但不位似
B.四边形ABCD与四边形BFGH位似但不相似
C.四边形ABCD与四边形BFGH位似,且位似比为l:
D.四边形ABCD与四边形BFGH位似,且位似比为l:2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影.已知桌面的直径为1.2 m,桌面距离地面1 m.若灯泡距离地面3 m,则地面上阴影部分的面积为 ( )
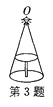
A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E为AD上一点,且AB=8,AE=3,BC=4,点P为AB上一动点,连接PC、PE,若PAE与PBC是相似三角形,则满足条件的点P的个数有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=
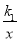 (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=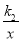 (x>0)的图象上,∠ABO=30°,求
(x>0)的图象上,∠ABO=30°,求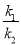 的值.
的值.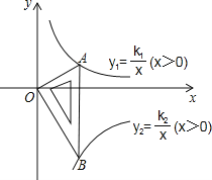
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
 的值.
的值.
相关试题

