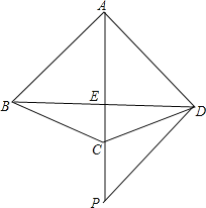
【题目】如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
(1)证明:∠BDC=∠PDC;
(2)若AC与BD相交于点E,AB=1,CE:CP=2:3,求AE的长.
参考答案:
【答案】(1)见解析(2)![]()
【解析】
(1)由三线合一可知AC⊥BD,然后利用等腰三角形的性质结合互余的定义得出∠BDC=∠PDC;
(2)首先过点C作CM⊥PD于点M,进而得出△CPM∽△APD,求出EC的长即可得出答案.
(1)证明:∵AB=AD,AC平分∠BAD,
∴AC⊥BD,
∴∠ACD+∠BDC=90°,
∵AC=AD,
∴∠ACD=∠ADC,
∴∠ADC+∠BDC=90°,
∵PD⊥AD,
∴∠ADC+∠PDC=90°,
∴∠BDC=∠PDC;
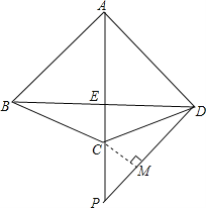
(2)解:过点C作CM⊥PD于点M,
∵∠BDC=∠PDC,
∴CE=CM,
∵∠CMP=∠ADP=90°,∠P=∠P,
∴△CPM∽△APD,
∴![]() =
=![]() ,
,
设CM=CE=x,
∵CE:CP=2:3,
∴PC=![]() x,
x,
∵AB=AD=AC=1,
∴![]() =
=![]() ,
,
解得:x=![]() ,
,
故AE=1-![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=
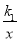 (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2=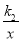 (x>0)的图象上,∠ABO=30°,求
(x>0)的图象上,∠ABO=30°,求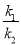 的值.
的值.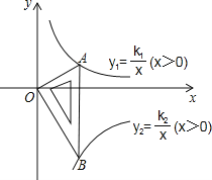
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E为ABCD的边BC延长线上一点,AE与BD交于点F,与DC交于点G.
(1)写出所有与△ABE相似的三角形,并选择其中一对相似三角形加以证明;
(2)若BC=2CE,求
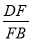 的值.
的值.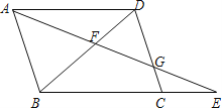
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y是x的反比例函数,且点A(3,5)在这个函数的图象上.
(1)求y与x之间的函数关系式;
(2)当点B(-5,m)也在这个反比例函数的图象上时,求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则
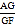 的值是( )
的值是( )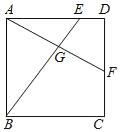
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】天山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游,推出了如下收费标准(如图所示):

某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游,共支付给旅行社旅游费用27000元,请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游?
相关试题

