【题目】如图,小明在山脚下的A处测得山顶N的仰角为45°,此时,他刚好与山底D在同一水平线上.然后沿着坡度为30°的斜坡正对着山顶前行110米到达B处,测得山顶N的仰角为60°.求山的高度.(结果精确到1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).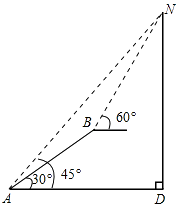
参考答案:
【答案】解:过点B作BF⊥DN于点F,过点B作BE⊥AD于点E,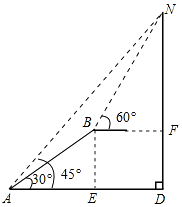
∵∠D=90°,
∴四边形BEDF是矩形,
∴BE=DF,BF=DE,
在Rt△ABE中,AE=ABcos30°=110× ![]() =55
=55 ![]() (米),
(米),
BE=ABsin30°= ![]() ×110=55(米),
×110=55(米),
设BF=x米,则AD=AE+ED=55 ![]() +x(米),
+x(米),
在Rt△BFN中,NF=BFtan60°= ![]() x(米),
x(米),
∵∠NAD=45°,
∴AD=DN,
∴DN=DF+NF=55+ ![]() x(米),
x(米),
即55 ![]() +x=
+x= ![]() x+55,
x+55,
解得:x=55,
∴DN=55+ ![]() x≈150(米),
x≈150(米),
答:山的高度约为150米.
【解析】过点B作BF⊥DN于点F,过点B作BE⊥AD于点E,根据余弦的定义求出AE,根据正弦的定义求出BE,设BF=x米,根据正切的定义求出NF,结合图形列出方程,解方程即可.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的课外阅读情况,就“我最喜爱的课外读物”对文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),并根据调查结果绘制了两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:

(1)这次被调查的学生共有多少名?
(2)请将条形统计图补充完整;并在扇形统计图中,计算出“其他类”所对应的圆心角的度数;
(3)若该校有2400名学生,请你估计该校喜爱“科普类”的学生有多少名. -
科目: 来源: 题型:
查看答案和解析>>【题目】用A、B两种规格的长方形纸板(如图1)无重合无缝隙的拼接可得如图2所示的周长为32cm的正方形,已知A种长方形的宽为1cm,则B种长方形的面积是( )
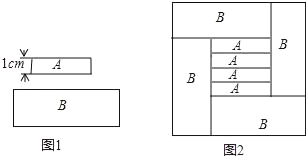
A. 10cm2 B. 12cm2 C. 14cm2 D. 16cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的2018年元月份的月历表中,任意框出表中竖列上四个数,这四个数的和可能是( )
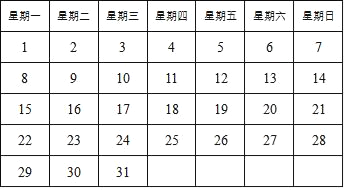
A. 86 B. 78 C. 60 D. 101
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,BC=7,将矩形ABCD绕点C逆时针旋转90°得到矩形A′B′CD′,点E、F分别是BD、B′D′的中点,则EF的长度为________cm.
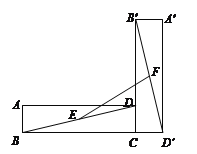
-
科目: 来源: 题型:
查看答案和解析>>【题目】铁路货运调度站有A、B两个信号灯,在灯这旁停靠着甲、乙、丙三列火车.它们中最长的车长与居中车长之差等于居中车长与最短车长之差,其中乙车的车长居中,最开始的时候,甲、丙两车车尾对齐,且车尾正好位于A信号灯处,而车头则冲着B信号灯的方向,乙车的车尾则位于B信号灯处,车头则冲着A的方向,现在,三列火车同时出发向前行驶,3秒之后三列火车的车头恰好相遇,再过9秒,甲车恰好超过丙车,而丙车也正好完全和乙车错开,请问:甲乙两车从车头相遇直到完全错开一共用了_____秒钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解全校2400名学生的阅读兴趣,从中随机抽查了部分同学,就“我最感兴趣的书籍”进行了调查:A.小说、B.散文、C.科普、D.其他(每个同学只能选择一项),进行了相关统计,整理并绘制出两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
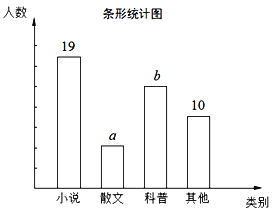

(1)本次抽查中,样本容量为______;
(2)a=______,b=______;
(3)扇形统计图中,其他类书籍所在扇形的圆心角是______°;
(4)请根据样本数据,估计全校有多少名学生对散文感兴趣.
相关试题

