【题目】如图,一次函数![]() 的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,![]() ),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,
【解析】
(1)先求出A、B两点的坐标,再由∠ABC=30°,求出AC的长,从而计算出面积;
(2)过P作PD⊥x轴,垂足为D,先求出梯形ODPB的面积和△AOB的面积之和,再减去△APD的面积,即是△APB的面积;根据△APB与△ABC面积相等,求得m的值;
(3)假设存在点Q,使△QAB是等腰三角形,求出Q点的坐标即可.
解:(1)∵一次函数的解析式为y=-![]() x+
x+![]() 函数图象与x轴、y轴分别交于点A、B,
函数图象与x轴、y轴分别交于点A、B,
∴A(1,0),B(0,![]() ),根据勾股定理可得:AB=2,
),根据勾股定理可得:AB=2,
在Rt△ABC, ∠ABC=30°,设AC=x,则BC=2x,由勾股定理得,4x2﹣x2=4,
解得x=![]() ,S△ABC=
,S△ABC=![]() =
=![]() ;
;
(2)过P作PD⊥x轴,垂足为D,

S△APB=S梯形ODPB+S△AOB﹣S△APD=![]() =
=![]() ,
,
![]() =
=![]() ,解得m=
,解得m=![]() ;
;
(3)∵AB=![]() =2,
=2,
∴当AQ=AB时,点Q1(3,0),Q2(﹣1,0),Q3(0,﹣![]() );
);
当AB=BQ时,点Q4(0,![]() +2),Q5(0,
+2),Q5(0,![]() ﹣2),Q2(﹣1,0);
﹣2),Q2(﹣1,0);
当AQ=BQ时,点Q6(0,![]() ),Q2(﹣1,0),
),Q2(﹣1,0),
综上可得:(0,![]() ),(0,
),(0,![]() ),(﹣1,0)(3,0),(0,
),(﹣1,0)(3,0),(0,![]() ),(0,
),(0,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A为
 边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sin
边上任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示sin 的值,错误的是( )
的值,错误的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
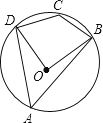
A.88°
B.92°
C.106°
D.136° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.图象必经过点(-1,5)
B.图象的两个分支分布在第二、四象限
C.y随x的增大而增大
D.若x>1,则-5<y<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,则BE等于( )
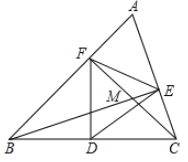
A. 14B. 13C. 12D. 11
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次数学课上,李老师让同学们独立完成课本第23页第七题选择题(2)如图 1,如果 AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=( )
A.180° B.270° C.360° D.540°
(1)请写出这道题的正确选项;
(2)在同学们都正确解答这道题后,李老师对这道题进行了改编:如图2,AB∥EF,请直接写出∠BAD,∠ADE,∠DEF之间的数量关系.
(3)善于思考的龙洋同学想:将图1平移至与图2重合(如图3所示),当AD,ED分别平分∠BAC,∠CEF时,∠ACE与∠ADE之间有怎样的数量关系?请你直接写出结果,不需要证明.
(4)彭敏同学又提出来了,如果像图4这样,AB∥EF,当∠ACD=90°时,∠BAC、∠CDE和∠DEF之间又有怎样的数量关系?请你直接写出结果,不需要证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题(尺规作图,不写作法,但保留作图痕迹).
如图,已知∠α和∠β,求作∠AOB,使∠AOB=∠α+∠β.
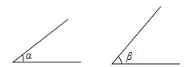
相关试题

