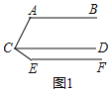
【题目】在一次数学课上,李老师让同学们独立完成课本第23页第七题选择题(2)如图 1,如果 AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=( )
A.180° B.270° C.360° D.540°
(1)请写出这道题的正确选项;
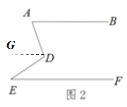
(2)在同学们都正确解答这道题后,李老师对这道题进行了改编:如图2,AB∥EF,请直接写出∠BAD,∠ADE,∠DEF之间的数量关系.
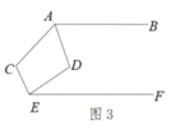
(3)善于思考的龙洋同学想:将图1平移至与图2重合(如图3所示),当AD,ED分别平分∠BAC,∠CEF时,∠ACE与∠ADE之间有怎样的数量关系?请你直接写出结果,不需要证明.
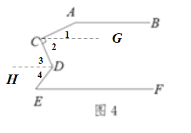
(4)彭敏同学又提出来了,如果像图4这样,AB∥EF,当∠ACD=90°时,∠BAC、∠CDE和∠DEF之间又有怎样的数量关系?请你直接写出结果,不需要证明.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)利用平行线的性质,即可得到![]() ,
,![]() ,进而得出
,进而得出![]() ;
;
(2)过![]() 作
作![]() ,利用平行线的性质,即可得到
,利用平行线的性质,即可得到![]() ,
,![]() ,进而得出
,进而得出![]() ;
;
(3)利用(1)可得![]() ,利用(2)可得
,利用(2)可得![]() ,根据
,根据![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,即可得到
,即可得到![]() ,化简即可得到
,化简即可得到![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(4)过![]() 作
作![]() ,过
,过![]() 作
作![]() ,则有
,则有![]() ,可得
,可得![]() ,
, ![]() ,
,![]() ,
,![]() ,则有
,则有![]() ,可求出
,可求出![]() ,利用
,利用![]() ,
,![]() ,得到
,得到![]() .
.
解:(1)
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即![]() ,
,
故选:![]() .
.
(2)![]() ,
,
如图,过![]() 作
作![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
(3)![]() ,
,
理由:由(1)可得,![]() ,
,
由(2)可得,![]() ,
,
又![]() ,
,![]() 分别平分
分别平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即![]() ,
,
![]() .
.
(4)![]() ,
,
理由:如图,过![]() 作
作![]() ,过
,过![]() 作
作![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
, ![]() ,
,![]() ,
,![]()
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即有:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.图象必经过点(-1,5)
B.图象的两个分支分布在第二、四象限
C.y随x的增大而增大
D.若x>1,则-5<y<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求△ABC的面积;
(2)如果在第二象限内有一点P(m,
 ),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;
),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值;(3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=60°,BE⊥AC,垂足为E,CF⊥AB,垂足为F,点D是BC的中点,BE,CF交于点M,如果CM=4,FM=5,则BE等于( )
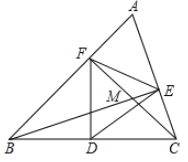
A. 14B. 13C. 12D. 11
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题(尺规作图,不写作法,但保留作图痕迹).
如图,已知∠α和∠β,求作∠AOB,使∠AOB=∠α+∠β.
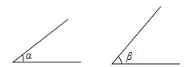
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.

解:∵∠A=∠F(已知)
∴AC∥DF( )
∴∠D=∠ ( )
又∵∠C=∠D(已知)
∴∠1=∠C(等量代换)
∴BD∥CE( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是小明同学在课堂上画的一个图形,AB∥CD,他要想得出∠1=∠2,那么还需要添加一个什么样的条件?
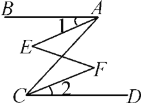
相关试题

