【题目】已知二次函数y=﹣ ![]() x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N. 
(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.
参考答案:
【答案】
(1)解:∵二次函数y=﹣ ![]() x2+bx+c的图象经过点A(2,0),
x2+bx+c的图象经过点A(2,0),
∴0=﹣ ![]() ×4+2b+c
×4+2b+c
∴c=2﹣2b
∴y=﹣ ![]() x2+bx+c=﹣
x2+bx+c=﹣ ![]() x2+bx+2﹣2b
x2+bx+2﹣2b
=﹣ ![]() (x﹣b)2+
(x﹣b)2+ ![]()
∴顶点M的坐标为(b, ![]() )
)
(2)解:∵tan∠MAN= ![]() =2
=2
∴MN=2AN.
∵M(b, ![]() )
)
∴N(b,0),
∴MN= ![]() (b﹣2)2
(b﹣2)2
①当点B在点N左侧时,AN=2﹣b,
∴ ![]() (b﹣2)2=2(2﹣b)
(b﹣2)2=2(2﹣b)
∴b=﹣2.不符合题意.
②当点B在点N右侧时,AN=b﹣2,
∴ ![]() (b﹣2)2=2(b﹣2)
(b﹣2)2=2(b﹣2)
∴b=6
∴二次函数的解析式为y=﹣ ![]() x2+6x﹣10
x2+6x﹣10
∴点C(0,﹣10),
∵点A、B关于直线MN对称,
∴点B(10,0).
∵OB=OC=10,
∴BC=10,∠OBC=45°,
过点A作AH⊥BC,垂足为H,
∵AB=8,∴AH=BH=4 ![]() ,∴CH=6
,∴CH=6 ![]()
∴tan∠ACB= ![]() =
= ![]() =
= ![]()
【解析】(1)由于二次函数过点A,从而可知c=2﹣2b,然后将c代入抛物线的解析式中即可求出抛物线的顶点坐标.(2)根据解析式可求出MN= ![]() (b﹣2)2,由于点B的位置不确定,需要分情况讨论,求出b的值,从而求出二次函数的解析式,然后求出B、C的坐标后即可求出tan∠ACB.
(b﹣2)2,由于点B的位置不确定,需要分情况讨论,求出b的值,从而求出二次函数的解析式,然后求出B、C的坐标后即可求出tan∠ACB.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G.
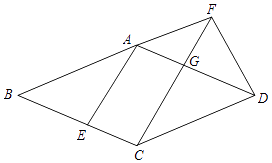
求证:
(1)FD=CG;
(2)CG2=FGFC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=
 πcm2;②
πcm2;②  ;③∠ACB=20°;④∠ADB=140°.错误的有( )
;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数
 的图象经过点D,四边形BCFG的面积为8,则k的值为( )
的图象经过点D,四边形BCFG的面积为8,则k的值为( )
A.16
B.20
C.24
D.28 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点,且经过A(m﹣1,n)和B(m+3,n),过点A,B分别作x轴的垂线,垂足记为M,N,则四边形AMNB的周长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形;

(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图4,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径OA的长为2,点B是⊙O上的动点,以AB为半径的⊙A与线段OB相交于点C,AC的延长线与⊙O相交于点D.设线段AB的长为x,线段OC的长为y.
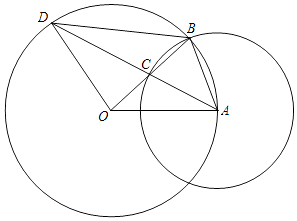
(1)求y关于x的函数解析式,并写出定义域;
(2)当四边形ABDO是梯形时,求线段OC的长.
相关试题

