【题目】已知:如图,在菱形ABCD中,点E在边BC上,点F在BA的延长线上,BE=AF,CF∥AE,CF与边AD相交于点G. 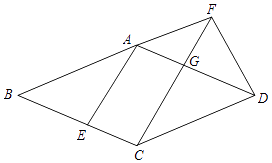
求证:
(1)FD=CG;
(2)CG2=FGFC.
参考答案:
【答案】
(1)证明:∵在菱形ABCD中,AD∥BC,
∴∠FAD=∠B,
在△ADF与△BAE中, 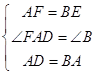 ,
,
∴△ADF≌△BAE,
∴FD=EA,
∵CF∥AE,AG∥CE,
∴EA=CG,
∴FD=CG
(2)解:∵在菱形ABCD中,CD∥AB,
∴∠DCF=∠BFC,
∵CF∥AE,
∴∠BAE=∠BFC,
∴∠DCF=∠BAE,
∵△ADF≌△BAE,
∴∠BAE=∠FDA,
∴∠DCF=∠FDA,
又∵∠DFG=∠CFD,
∴△FDG∽△FCD,
∴ ![]() ,FD2=FGFC,
,FD2=FGFC,
∵FD=CG,
∴CG2=FGFC
【解析】(1)根据菱形的性质得到∠FAD=∠B,根据全等三角形的性质得到FD=EA,于是得到结论;(2)根据菱形的性质得到∠DCF=∠BFC,根据平行线的性质得到∠BAE=∠BFC,根据全等三角形的性质得到∠BAE=∠FDA,等量代换得到∠DCF=∠FDA,根据相似三角形的判定和性质即可得到结论.
【考点精析】通过灵活运用菱形的性质和相似三角形的判定与性质,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AB=AC,AC腰上的中线BD将三角形周长分为15和21两部分,则这个三角形的底边长为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各个选项中的网格都是边长为1的小正方形,利用函数的图象解方程
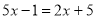 ,其中正确的是( )
,其中正确的是( )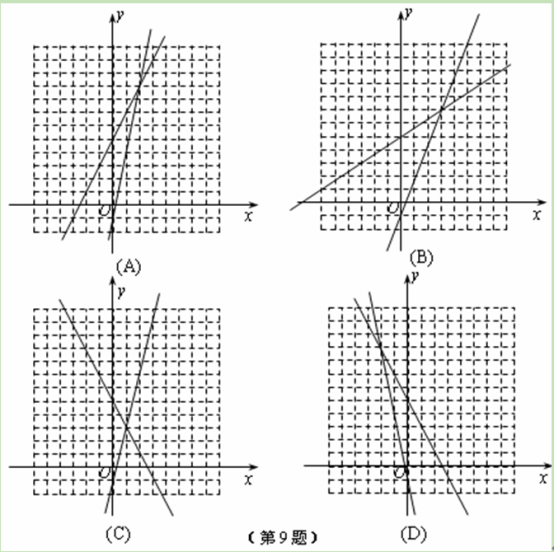
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形DEF是三角形ABC平移所得,观察图形:(1)点A的对应点是点 ,点B的对应点是点 ,点C的对应点是点 ;(2)线段AD,BE,CF叫做对应点间的连线,这三条线段之间有什么关系呢?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分别在优弧与劣弧上.则下列结论:①S扇形AOB=
 πcm2;②
πcm2;②  ;③∠ACB=20°;④∠ADB=140°.错误的有( )
;③∠ACB=20°;④∠ADB=140°.错误的有( )
A.0个
B.1个
C.2个
D.3个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,平行四边形OABC的顶点C(3,4),边OA落在x正半轴上,P为线段AC上一点,过点P分别作DE∥OC,FG∥OA交平行四边形各边如图.若反比例函数
 的图象经过点D,四边形BCFG的面积为8,则k的值为( )
的图象经过点D,四边形BCFG的面积为8,则k的值为( )
A.16
B.20
C.24
D.28 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣
 x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N.
x2+bx+c的图象与x轴的正半轴相交于点A(2,0)和点B、与y轴相交于点C,它的顶点为M、对称轴与x轴相交于点N. 
(1)用b的代数式表示顶点M的坐标;
(2)当tan∠MAN=2时,求此二次函数的解析式及∠ACB的正切值.
相关试题

