Question

【题目】如图，已知⊙O的半径OA的长为2，点B是⊙O上的动点，以AB为半径的⊙A与线段OB相交于点C，AC的延长线与⊙O相交于点D．设线段AB的长为x，线段OC的长为y．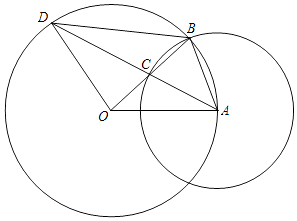
（1）求y关于x的函数解析式，并写出定义域；
（2）当四边形ABDO是梯形时，求线段OC的长．

Answer 1

【答案】
（1）解：在⊙O与⊙A中，

∵OA=OB，AB=AC，

∴∠ACB=∠ABC=∠OAB，

∴△ABC∽△OAB，

∴ = ，

∴ = ，

∴BC= x2，

∵OC=OB﹣BC，

∴y关于x的函数解析式y=2﹣ x2，

定义域为0＜x＜2．

（2）解：①当OD∥A B时，

∴ = ，

∴ = ，

整理得x2+2x﹣4=0，

∴x=﹣1 （负值舍去），

∴AB= ，这时AB≠OD，符合题意．

∴OC=2﹣ x2=2﹣ （ ﹣1）2= ﹣1．

②当BD∥OA时，设∠ODA=α，

∵BD∥OA，OA=OD，

∴∠BDA=∠OAD=∠ODA=α，

又∵OB=OD，∴∠BOA=∠OBD=∠ODB=2α，

∵AB=AC，OA=OB，

∴∠OAB=∠ABC=∠ACB=∠COA+∠CAO=3α，

∵∠AOB+∠OAB+∠OBA=180°，

∴2α+3α+3α=180°，

∴α=22.5°，∠BOA=45°，

∴∠ODB=∠OBD=45°，∠BOD=90°，

∴BD=2 ，

∵BD∥OA，

∴ = ，

∴ = ，

∴y=2 ﹣2．OC=2 ﹣2，

由于BD≠OA，OC=2 ﹣2符合题意．

∴当四边形ABDO是梯形时，线段OC的长为 ﹣1或2 ﹣2．

【解析】（1）由△ABC∽△OAB，推出 = ，可得 = ，推出BC= x2，由OC=OB﹣BC，可得y关于x的函数解析式y=2﹣ x2；（2）分两种情形讨论①当OD∥A B时，②当BD∥OA时，分别想办法构建方程解决问题；