【题目】问题提出
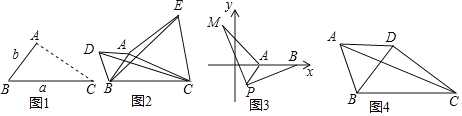
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
参考答案:
【答案】(1)CB的延长线上,a+b;(2)①CD=BE,②9;(3)P(2﹣![]() ,
,![]() )(4)AC的最大值为2
)(4)AC的最大值为2![]() +2
+2![]()
【解析】试题分析:(1)根据点A位于CB的延长线上时,线段AC的长取得最大值,即可得到结论;
(2)①根据等边三角形的性质得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根据全等三角形的性质得到CD=BE;②由于线段BE长的最大值=线段CD的最大值,根据(1)中的结论即可得到结果;
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,得到△APN是等腰直角三角形,根据全等三角形的性质得到PN=PA=2,BN=AM,根据当N在线段BA的延长线时,线段BN取得最大值,即可得到最大值为2![]() +3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论;
+3;过P作PE⊥x轴于E,根据等腰直角三角形的性质,即可得到结论;
(4)如图4中,以BC为边作等边三角形△BCM,由△ABC≌△DBM,推出AC=MD,推出欲求AC的最大值,只要求出DM的最大值即可,由BC=4![]() =定值,∠BDC=90°,推出点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大;
=定值,∠BDC=90°,推出点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大;
试题解析:解:(1)∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.故答案为:CB的延长线上,a+b;
(2)①CD=BE,理由:∵△ABD与△ACE是等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB.在△CAD与△EAB中,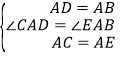 ,∴△CAD≌△EAB(SAS),∴CD=BE;
,∴△CAD≌△EAB(SAS),∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,∴由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,∴最大值为BD+BC=AB+BC=3+6=9;
(3)如图1,连接BM.∵将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,则△APN是等腰直角三角形,∴PN=PA=2,BN=AM.∵A的坐标为(2,0),点B的坐标为(5,0),∴OA=2,OB=5,∴AB=3,∴线段AM长的最大值=线段BN长的最大值,∴当N在线段BA的延长线时,线段BN取得最大值,最大值=AB+AN.∵AN=![]() AP=2
AP=2![]() ,∴最大值为2
,∴最大值为2![]() +3;
+3;
如图2,过P作PE⊥x轴于E.∵△APN是等腰直角三角形,∴PE=AE=![]() ,∴OE=BO﹣AB﹣AE=5﹣3﹣
,∴OE=BO﹣AB﹣AE=5﹣3﹣![]() =2﹣
=2﹣![]() ,∴P(2﹣
,∴P(2﹣![]() ).
).
(4)如图4中,以BC为边作等边三角形△BCM.∵∠ABD=∠CBM=60°,∴∠ABC=∠DBM.∵AB=DB,BC=BM,∴△ABC≌△DBM,∴AC=MD,∴欲求AC的最大值,只要求出DM的最大值即可.∵BC=4![]() =定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2
=定值,∠BDC=90°,∴点D在以BC为直径的⊙O上运动,由图象可知,当点D在BC上方,DM⊥BC时,DM的值最大,最大值=2![]() +2
+2![]() ,∴AC的最大值为2
,∴AC的最大值为2![]() +2
+2![]() .
.
-
科目: 来源: 题型:
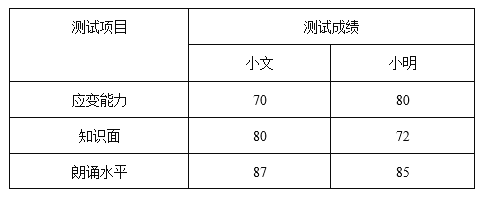
查看答案和解析>>【题目】学校广播站要招聘一名播音员,需考查应聘学生的应变能力、知识面、朗读水平三个项目,决赛中,小文和小明两位同学的各项成绩如下表,评委计算三项测试的平均成绩,发现小明与小文的相同.
(1)评委按应变能力占10%,知识面占40%,朗诵水平占50%计算加权平均数,作为最后评定的总成绩,成绩高者将被录用,小文和小明谁将被录用?
(2)若(1)中应变能力占x%,知识面占(50﹣x)%,其中0<x<50,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线AD对应的函数关系式为y=﹣2x﹣2,与抛物线交于点A(在x轴上),点D.抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,﹣6).
(1)求抛物线的解析式;
(2)如图2,连结CD,过点D作x轴的垂线,垂足为点E,直线AD与y轴交点为F,若点P由点D出发以每秒1个单位的速度沿DE边向点E移动,1秒后点Q也由点D出发以每秒3个单位的速度沿DC,CO,OE边向点E移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒,当PQ⊥DF时,求t的值;(图3为备用图)
(3)如果点M是直线BC上的动点,是否存在一个点M,使△ABM中有一个角为45°?如果存在,直接写出所有满足条件的M点坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三辆汽车经过某收费站下高速时,在2个收费通道A,B中,可随机选择其中的一个通过.
(1)三辆汽车经过此收费站时,都选择A通道通过的概率是 ;
(2)求三辆汽车经过此收费站时,至少有两辆汽车选择B通道通过的概率.
-
科目: 来源: 题型:
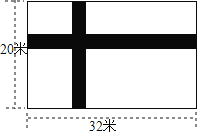
查看答案和解析>>【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:
(1)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )

A.2个 B.3个 C.4个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(a,m)、B(2a,n)是反比例函数y=
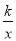 (k>0)与一次函数y=-
(k>0)与一次函数y=- x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.
x+b图象上的两个不同的交点,分别过A、B两点作x轴的垂线,垂足分别为C、D,连结OA、OB,若已知1≤a≤2,则求S△OAB的取值范围.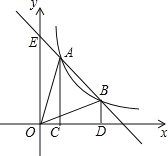
相关试题

