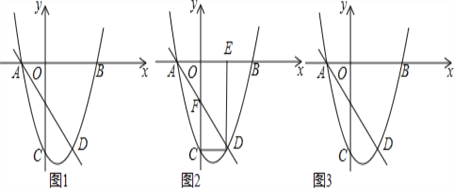
【题目】如图1,直线AD对应的函数关系式为y=﹣2x﹣2,与抛物线交于点A(在x轴上),点D.抛物线与x轴另一交点为B(3,0),抛物线与y轴交点C(0,﹣6).
(1)求抛物线的解析式;
(2)如图2,连结CD,过点D作x轴的垂线,垂足为点E,直线AD与y轴交点为F,若点P由点D出发以每秒1个单位的速度沿DE边向点E移动,1秒后点Q也由点D出发以每秒3个单位的速度沿DC,CO,OE边向点E移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒,当PQ⊥DF时,求t的值;(图3为备用图)
(3)如果点M是直线BC上的动点,是否存在一个点M,使△ABM中有一个角为45°?如果存在,直接写出所有满足条件的M点坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)y=2x2﹣4x﹣6(2)当t=2时,有PQ⊥DF(3)点M(7,8),(![]() ,
,![]() ),(
),( ![]() ,
,![]() ),(
),(![]() ,
,![]() )
)
【解析】试题分析:(1)求出点A坐标,把A、B、C三点代入抛物线解析式解方程组即可.
(2)分三种情形讨论①当Q点在CD上时②点Q在CO上时③点Q在OE上时,利用相似三角形的性质路程方程求出t,并且判断是否符合题意即可.
(3)分三种情况:①当∠MAB=45°且M在x轴上方时,则直线过A和P(0, 1),求出直线AP的解析式和直线AP与直线BC的交点即可;
②当∠MAB=45°且M在x轴下方时,则直线过A和Q(0,-1),类似可求M的坐标;
③若∠AMB=45°,过A作AP⊥BC于P,则△APM是等腰直角三角形,得到AP=PM.求出直线AP的解析式,然后求出直线AP和直线CB的交点P的坐标,由MP=AP,用两点间的距离公式,列方程求解即可.
试题解析:解:(1)令y=0,则﹣2x﹣2=0,解得:x=﹣1,所以点A坐标(﹣1,0),设抛物线解析式为y=ax2+bx+c.∵A(﹣1,0)、B(3,0)、C(0,﹣6)在抛物线上,∴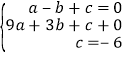 ,解得:
,解得: ,∴抛物线解析式为y=2x2﹣4x﹣6.
,∴抛物线解析式为y=2x2﹣4x﹣6.
(2)y=2x﹣2,令x=0,y=﹣2,∴F(0,﹣2),由![]() 解得
解得![]() 或
或![]() ,∴点D坐标(2,﹣6).∵点C(0,﹣6),∴CD⊥CF,∴∠DCF=90°,由题意:P点移动的路程为DP=t,Q点移动的路程为3(t﹣1)=3t﹣3,当Q点在CD上时,即0<3t﹣3≤2时,1<t≤
,∴点D坐标(2,﹣6).∵点C(0,﹣6),∴CD⊥CF,∴∠DCF=90°,由题意:P点移动的路程为DP=t,Q点移动的路程为3(t﹣1)=3t﹣3,当Q点在CD上时,即0<3t﹣3≤2时,1<t≤![]() 时,如图1中,若PQ⊥DF,则有Rt△QDP∽Rt△FCD,
时,如图1中,若PQ⊥DF,则有Rt△QDP∽Rt△FCD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,∴t=3,3>
,∴t=3,3>![]() ,∴此时t不合题意.
,∴此时t不合题意.
当点Q在CO上时,2<3t﹣3≤8,![]() <t≤
<t≤![]() 时,如图2中,过点P作PK⊥OC于K,
时,如图2中,过点P作PK⊥OC于K,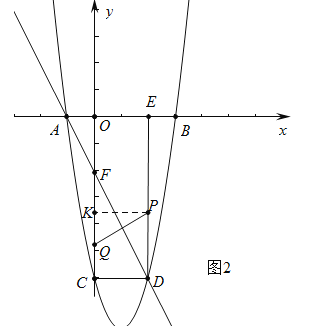
∴CK=PD=t,CQ=3(t﹣1)﹣2=3t﹣5,若PQ⊥DF,则有Rt△PKQ∽Rt△FCD,∴![]() ,即
,即![]() =
=![]() ,∴t=2.∵
,∴t=2.∵![]() <t≤
<t≤![]() ,∴t=2符合题意.
,∴t=2符合题意.
当点Q在OE上时,即8≤3t﹣3≤10,![]() ≤t≤
≤t≤![]() 时,如图3中,
时,如图3中,
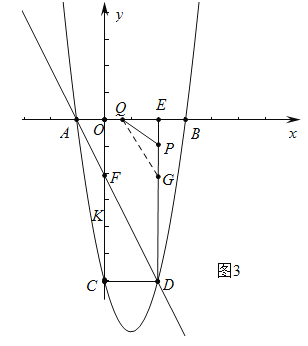
若PQ⊥DF,过点Q作QG∥DF交DE于G,则QG⊥QP,即∠GQP=90°,∴∠QPE>90°,这与△QPE内角和为180°矛盾,此时PQ不与DF垂直.
综上所述:当t=2时,有PQ⊥DF.
(3)分三种情况讨论:
①当∠MAB=45°且M在x轴上方时.∵A(-1,0)在y轴上取点P(0,1)直线AP交在线CB于M,则∠MAB=45°,如图4.易求直线AP为y=x+1,易求直线BC的解析式为:y=2x-6,解方程组:![]() ,解得:
,解得:![]() ,∴M(7,8);
,∴M(7,8);
②当∠MAB=45°且M在x轴下方时.在y轴上取点Q(0,-1)直线AQ交在线CB于M′,则∠M′AB=45°,类似可求M(![]() ,
,![]() );
);
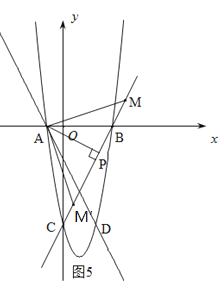
③若∠AMB=45°,过A作AP⊥BC于P,则△APM是等腰直角三角形,∴AP=PM.如图5.∵AP⊥CB,∴直线AP为![]() ,解方程组:
,解方程组: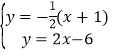 ,解得:
,解得: ,∴P(
,∴P(![]() ,
,![]() ),∴AP=
),∴AP=![]() =
=![]() .设M(a,2a-6),则MP=AP,∴
.设M(a,2a-6),则MP=AP,∴![]() =
=![]() ,整理得:25a2-110a+57=0,∴(5a-19)(5a-3)=0,解得:a=
,整理得:25a2-110a+57=0,∴(5a-19)(5a-3)=0,解得:a=![]() 或a=
或a=![]() ,∴M(
,∴M(![]() ,
,![]() )或M′(
)或M′(![]() ,
,![]() ).
).
综上所述:存在一个点M,使△ABM中有一个角为45°,M的坐标为:M(7,8)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某运输部门规定:办理托运,当一件物品的重量不超过
 千克时,需付基础费
千克时,需付基础费 元和保险费
元和保险费 元;为了限制过重物品的托运,当一件物品的重量超过
元;为了限制过重物品的托运,当一件物品的重量超过 千克时,除了付以上基础费和保险费外,超过部分每千克还需付
千克时,除了付以上基础费和保险费外,超过部分每千克还需付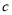 元的超重费.设某件物品的重量为
元的超重费.设某件物品的重量为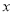 千克,支付费用为
千克,支付费用为 元.
元.(1)当
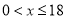 时,
时, ______________(用式子表示);
______________(用式子表示);当
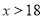 时,
时, ______________(用式子表示);
______________(用式子表示);(2)甲、乙、丙三人各托运一件物品,物品的重量与支付费用如下表所示:
托运人
物品重量/千克
支付费用/元
甲
14
33
乙
20
39
丙
30
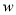
根据以上提供的信息确定
 的值,并计算出丙所支付的费用
的值,并计算出丙所支付的费用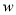 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】工厂接到订单,需要边长为(a+3)和3的两种正方形卡纸.
(1)仓库只有边长为(a+3)的正方形卡纸,现决定将部分边长为(a+3)的正方形纸片,按图甲所示裁剪得边长为3的正方形.
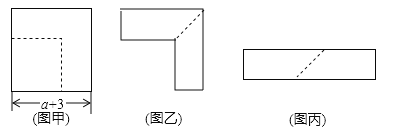
①如图乙,求裁剪正方形后剩余部分的面积(用含a代数式来表示);
②剩余部分沿虚线又剪拼成一个如图丙所示长方形(不重叠无缝隙),则拼成的长方形的边长多少?(用含a代数式来表示);
(2)若将裁得正方形与原有正方形卡纸放入长方体盒子底部,按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),盒子底部中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2测得盒子底部长方形长比宽多3,则S2﹣S1的值为 .

-
科目: 来源: 题型:
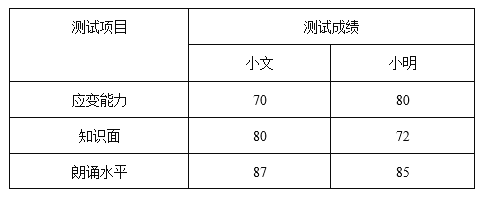
查看答案和解析>>【题目】学校广播站要招聘一名播音员,需考查应聘学生的应变能力、知识面、朗读水平三个项目,决赛中,小文和小明两位同学的各项成绩如下表,评委计算三项测试的平均成绩,发现小明与小文的相同.
(1)评委按应变能力占10%,知识面占40%,朗诵水平占50%计算加权平均数,作为最后评定的总成绩,成绩高者将被录用,小文和小明谁将被录用?
(2)若(1)中应变能力占x%,知识面占(50﹣x)%,其中0<x<50,其它条件都不改变,使另一位选手被录用,请直接写出一个你认为合适的x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三辆汽车经过某收费站下高速时,在2个收费通道A,B中,可随机选择其中的一个通过.
(1)三辆汽车经过此收费站时,都选择A通道通过的概率是 ;
(2)求三辆汽车经过此收费站时,至少有两辆汽车选择B通道通过的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示).
问题探究
(2)点A为线段BC外一动点,且BC=6,AB=3,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE,找出图中与BE相等的线段,请说明理由,并直接写出线段BE长的最大值.
问题解决:
(3)①如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,求线段AM长的最大值及此时点P的坐标.
②如图4,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4
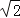 ,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.
,若对角线BD⊥CD于点D,请直接写出对角线AC的最大值.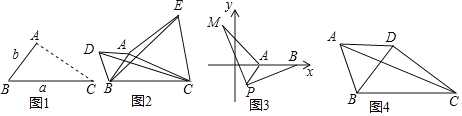
-
科目: 来源: 题型:
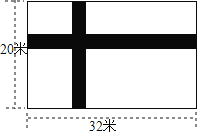
查看答案和解析>>【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
相关试题

