搜索
【题目】如图所示的二次函数y=ax2+bx+c的图象中，刘星同学观察得出了下面四条信息：
（1）b2-4ac＞0；（2）c＞1；（3）2a-b＜0；（4）a+b+c＜0．你认为其中错误的有（ ）
A．2个 B．3个 C．4个 D．1个
参考答案：
【答案】D．
【解析】
试题解析：（1）根据图示知，该函数图象与x轴有两个交点，
∴△=b2-4ac＞0；
故本选项正确；
（2）由图象知，该函数图象与y轴的交点在点（0，1）以下，
∴c＜1；
故本选项错误；
（3）由图示，知
对称轴x=-
＞-1；
又函数图象的开口方向向下，
∴a＜0，
∴-b＜-2a，即2a-b＜0，
故本选项正确；
（4）根据图示可知，当x=1，即y=a+b+c＜0，
∴a+b+c＜0；
故本选项正确；
故选D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】三辆汽车经过某收费站下高速时，在2个收费通道A，B中，可随机选择其中的一个通过．
（1）三辆汽车经过此收费站时，都选择A通道通过的概率是 ；
（2）求三辆汽车经过此收费站时，至少有两辆汽车选择B通道通过的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出
（1）如图1，点A为线段BC外一动点，且BC=a，AB=b，填空：当点A位于 时，线段AC的长取得最大值，且最大值为 （用含a，b的式子表示）．
问题探究
（2）点A为线段BC外一动点，且BC=6，AB=3，如图2所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE，找出图中与BE相等的线段，请说明理由，并直接写出线段BE长的最大值．
问题解决：
（3）①如图3，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（5，0），点P为线段AB外一动点，且PA=2，PM=PB，∠BPM=90°，求线段AM长的最大值及此时点P的坐标．
②如图4，在四边形ABCD中，AB=AD，∠BAD=60°，BC=4
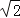，若对角线BD⊥CD于点D，请直接写出对角线AC的最大值．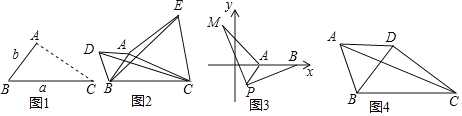
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，宽为20米，长为32米的长方形地面上，修筑宽度为x米的两条互相垂直的小路，余下的部分作为耕地，如果要在耕地上铺上草皮，选用草皮的价格是每平米a元，
（1）求买草皮至少需要多少元？（用含a，x的式子表示）
（2）计算a＝40，x＝2时，草皮的费用．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A（a，m）、B（2a，n）是反比例函数y=
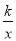（k＞0）与一次函数y=-
x+b图象上的两个不同的交点，分别过A、B两点作x轴的垂线，垂足分别为C、D，连结OA、OB，若已知1≤a≤2，则求S△OAB的取值范围．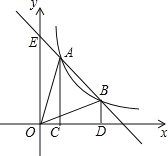
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知反比例函数
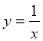和一次函数y=-x+a-1（a为常数）（1）当a＝5时，求反比例函数与一次函数的交点坐标（5分）
（2）是否存在实数a，使反比例函数与一次函数有且只有一个交点，如果存在，求出实数a，如果不存在，说明理由（5分）
-
科目： 来源： 题型：
查看答案和解析>>【题目】“端午节”期间，小明一家自驾游去了离家200km的某地，如图是他们离家的距离y（km）与汽车行驶时间x（h）之间的函数图象．根据图象，解答下列问题：
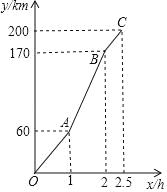
（1）点A的实际意义是 ；
（2）求出线段AB的函数表达式；
（3）他们出发2.3h时，距目的地还有多少km？
相关试题
