【题目】如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,那么△A2B2C2的面积是( )
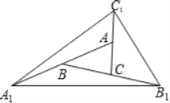
A. 7 B. 14 C. 49 D. 50
参考答案:
【答案】C
【解析】
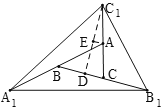
如图:过C1作C1D⊥BB1,过A作AE//BB1,由C1A=CA可得EC1=DE,由BC=B1C可知S△B1CC1=2S△ABC,同理可得S△A1AC1=2S△ABC,S△A1BB1=2S△ABC,即可求得S△A1B1C1=7S△ABC,同理可得S△A2B2C2=7S△A1B1C1,根据△ABC面积为1即可得答案.
如图:过C1作C1D⊥BB1,过A作AE//BB1,
∵C1A=CA,AE//BB1,
∴EC1=DE,即C1D=2DE,
∵C1D⊥BB1,AE//BB1,
∴C1D和DE分别是△B1CC1和△ABC的高,
∵BC=B1C,
∴S△B1CC1=2S△ABC,
同理:S△A1AC1=2S△ABC,S△A1BB1=2S△ABC,
∴S△A1B1C1=S△B1CC1+S△A1AC1+S△A1BB1+S△ABC=7S△ABC=7,
同理:S△A2B2C2=7S△A1B1C1=7×7=49.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)如图①,∠AFH和∠CHF的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.
(1)若∠AFH=60°,∠CHF=50°,则∠EOF=_____度,∠FOH=_____度.
(2)若∠AFH+∠CHF=100°,求∠FOH的度数.
(拓展)如图②,∠AFH和∠CHI的平分线交于点O,EG经过点O且平行于FH,分别与AB、CD交于点E、G.若∠AFH+∠CHF=α,直接写出∠FOH的度数.(用含a的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+8(a≠0)与x轴交于A(﹣2,0),B两点,与y轴交于C点,tan∠ABC=2.
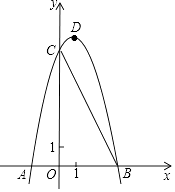
(1)求抛物线的表达式及其顶点D的坐标;
(2)过点A、B作x轴的垂线,交直线CD于点E、F,将抛物线沿其对称轴向上平移m个单位,使抛物线与线段EF(含线段端点)只有1个公共点.求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)
如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.

(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=30°,∠B=62°,CE平分∠ACB,CD⊥AB于D,DF⊥CE于F,求∠CDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某“数学兴趣小组”根据学习函数的经验,对函数y=
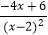 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整: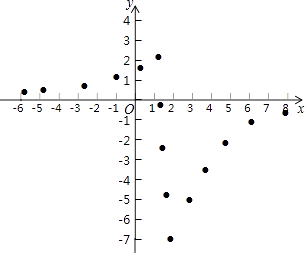
(1)该函数的自变量x的取值范围是;
(2)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
(3)结合画出的函数图象,写出该函数的一条性质: . -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂计划生产A、B两种产品共50件.已知A产品每件可获利润1200元,B产品每件可获利润700元,设生产两种产品的获利总额为y(元),生产A产品x(件).
(1)写出y与x之间的函数关系式;
(2)若生产A、B两种产品的件数均不少于10件,求总利润的最大值.
相关试题

