【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果 ![]() =
= ![]() ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 ![]() =
= ![]() ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.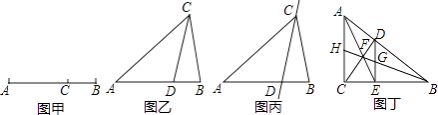
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
参考答案:
【答案】
(1)解:点D是AB边上的黄金分割点.理由如下:
∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵CD是角平分线,
∴∠ACD=∠BCD=36°,
∴∠A=∠ACD,
∴AD=CD,
∵∠CDB=180°﹣∠B﹣∠BCD=72°,
∴∠CDB=∠B,
∴BC=CD,
∴BC=AD.
在△BCD与△BCA中,∠B=∠B,∠BCD=∠A=36°,
∴△BCD∽△BAC,
∴ ![]() ,
,
∴ ![]() ,
,
∴点D是AB边上的黄金分割点.
(2)直线CD是△ABC的黄金分割线.理由如下:
证明:设△ABC中,AB边上的高为h,则S△ABC= ![]() ABh,S△ACD=
ABh,S△ACD= ![]() ADh,S△BCD=
ADh,S△BCD= ![]() BDh,
BDh,
∴S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,
由(1)知,点D是AB边上的黄金分割点,
∴ ![]() ,
,
∴S△ACD:S△ABC=S△BCD:S△ACD,
∴CD是△ABC的黄金分割线.
(3)解:直线BH不是△ABC的黄金分割线.理由如下:
∵DE∥AC,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴AH2=HC2,
∴AH=HC,
∴S△BHA=S△BHC= ![]() S△ABC,
S△ABC,
∴BH不是△ABC的黄金分割线.
【解析】(1)根据等边对等角得出∠B=∠ACB=72°,根据角平分线的定义及等量代换得出∠A=∠ACD,进而根据等角对等边得出AD=CD,BC=CD,从而得出BC=AD.然后判断出△BCD∽△BAC,根据相似三角形对应边成比例得出![]() =
=![]() ,从而得出
,从而得出![]() =
=![]() ,从而得出结论点D是AB边上的黄金分割点;
,从而得出结论点D是AB边上的黄金分割点;
(2)设△ABC中,AB边上的高为h,根据三角形的面积公式,则S△ABC= ![]() ABh,S△ACD=
ABh,S△ACD= ![]() ADh,S△BCD=
ADh,S△BCD= ![]() BDh,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,点D是AB边上的黄金分割点,故
BDh,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,点D是AB边上的黄金分割点,故![]() =
=![]() ,根据等量代换得S△ACD:S△ABC=S△BCD:S△ACD,从而得出结论;
,根据等量代换得S△ACD:S△ABC=S△BCD:S△ACD,从而得出结论;
(3)直线BH不是△ABC的黄金分割线.理由如下:根据平行线分线段成比例定理得出AH2=HC2,故AH=HC,从而S△BHA=S△BHC= ![]() S△ABC,得出结论BH不是△ABC的黄金分割线.
S△ABC,得出结论BH不是△ABC的黄金分割线.
【考点精析】通过灵活运用三角形的面积和平行线分线段成比例,掌握三角形的面积=1/2×底×高;三条平行线截两条直线,所得的对应线段成比例即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=30°,点M,N在射线OA上(都不与点O重合),且MN=2,点P在射线OB上,若△MPN为等腰直角三角形,则PO的长为 ___.

-
科目: 来源: 题型:
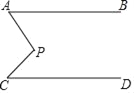
查看答案和解析>>【题目】如图,AB∥CD,∠A=50°,∠C=45°,求∠P的度数.
下面提供三种思路:
(1)过P作FG∥AB
(2)延长AP交直线CD于M;
(3)延长CP交直线AB于N.
请选择两种思路,求出∠P的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】研学活动继承和发展了我国传统游学“读万卷书,行万里路”的教育理念和人文精神,成为教育的新内容和新方式.朝阳区一所中学组织学生去某市进行研学活动,原计划乘坐特快列车前往,为了节省时间,现改为乘坐高铁列车前往.已知北京与该市的距离约为1200千米,高铁列车的平均速度是特快列车的平均速度的2.4倍,且乘坐高铁列车所用时间比乘坐特快列车所用时间少用7小时,求特快列车的平均速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点A出发,沿AB方向匀速运动,速度为1cm/s;过点P作直线PF∥AD,PF交CD于点F,过点F作EF⊥BD,且与AD、BD分别交于点E、Q;连接PE,设点P的运动时间为t(s)(0<t<10).
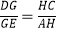 解答下列问题:
解答下列问题:
(1)填空:AB= cm;
(2)当t为何值时,PE∥BD;
(3)设四边形APFE的面积为y(cm2)
①求y与t之间的函数关系式;
②若用S表示图形的面积,则是否存在某一时刻t,使得S四边形APFE=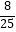 S菱形ABCD?若存在,求出t的值;若不存在,请说明理由.
S菱形ABCD?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AC是⊙O的直径,∠BDC=40°(点D在⊙O上),则∠ACB=( )

A.20°
B.30°
C.40°
D.50° -
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

相关试题

