搜索
【题目】如图，∠AOB=30°，点M，N在射线OA上(都不与点O重合)，且MN=2，点P在射线OB上，若△MPN为等腰直角三角形，则PO的长为 ___．
参考答案：
【答案】2或4
【解析】
△MPN是等腰直角三角形，则有三种可能：∠PMN是直角，∠MPN是直角，∠PNM是直角，根据角度和边长的关系，分三种情况一一讨论，求出PO的长度.
情况一，∠PMN＝90°，则PM＝MN=2.在△OPM中，∠PMO＝90°，∠O＝30°，所以PO＝2×PM＝4.
情况二，∠MPN＝90°，则PN＝PM＝
.过P做PC垂直OA于C，易知PC＝1.△OCP中，∠O＝30°，∠PCO＝90°，所以OP＝2×PC＝2.
情况三，∠PNM＝90°，由于OB上不存在这样的P点满足条件，所以该情况不会出现.
综上，PO的长度为2或4.
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角” (如图)就是一例.这个三角形给出了
(n=1，2，3，4，5，6)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如，在三角形中第三行的三个数1，2，1，恰好对应
展开式中各项的系数；第五行的五个数1，4，6，4，1，恰好对应着
展开式中各项的系数，等等.
有如下三个结论：
①当a=1,b=1时，代数式
的值是1；②当a=-1,b=2时，代数式
的值是1；③当代数式
的值是1时，a的值是-2或-4.上述结论中，所有正确结论的序号为( )
A. ①② B. ② C. ③ D. ②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2
(2)(x﹣5)(2x+5)+2x(3﹣x)
(3)(﹣1)2016+(﹣
)﹣2﹣(3.14﹣π)0(4)运用乘法公式计算：1122﹣113×111
-
科目： 来源： 题型：
查看答案和解析>>【题目】设m是不小于﹣1的实数，使得关于x的方程x2+2（m﹣2）x+m2﹣3m+3=0有两个实数根x1 ， x2 ．
（1）若x12+x22=2，求m的值；
（2）代数式
+ 
有无最大值？若有，请求出最大值；若没有，请说明理由． -
科目： 来源： 题型：
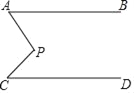
查看答案和解析>>【题目】如图，AB∥CD，∠A＝50°，∠C＝45°，求∠P的度数．
下面提供三种思路：
(1)过P作FG∥AB
(2)延长AP交直线CD于M；
(3)延长CP交直线AB于N．
请选择两种思路，求出∠P的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】研学活动继承和发展了我国传统游学“读万卷书，行万里路”的教育理念和人文精神，成为教育的新内容和新方式．朝阳区一所中学组织学生去某市进行研学活动，原计划乘坐特快列车前往，为了节省时间，现改为乘坐高铁列车前往．已知北京与该市的距离约为1200千米，高铁列车的平均速度是特快列车的平均速度的2.4倍，且乘坐高铁列车所用时间比乘坐特快列车所用时间少用7小时，求特快列车的平均速度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图甲，点C将线段AB分成两部分（AC＞BC），如果
= 
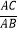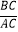，那么称点C为线段AB的黄金分割点．某数学兴趣小组在进行课题研究时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成面积分别为S1 ， S2（S1＞S2）的两部分，如果 
= 
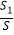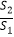，那么称直线l为该图形的黄金分割线．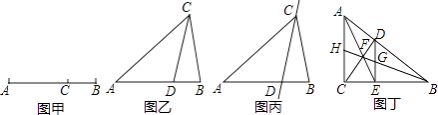
（1）如图乙，在△ABC中，∠A=36°，AB=AC，∠ACB的平分线交AB于点D，请问点D是否是AB边上的黄金分割点，并证明你的结论；
（2）若△ABC在（1）的条件下，如图丙，请问直线CD是不是△ABC的黄金分割线，并证明你的结论；
（3）如图丁，在Rt△ABC中，∠ACB=90°，D为斜边AB上的一点，（不与A，B重合）过D作DE⊥BC于点E，连接AE，CD相交于点F，连接BF并延长，与DE，AC分别交于点G，H．请问直线BH是直角三角形ABC的黄金分割线吗？并说明理由．
相关试题
