【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

参考答案:
【答案】(1) a2﹣b2,(a+b)(a﹣b),平方差,a2﹣b2=(a+b)(a﹣b);(2)①5;②2128.
【解析】
(1)根据两个图形中阴影部分的面积相等,即可列出等式;
(2)①把x2﹣4y2利用(1)的结论写成两个式子相乘的形式,然后把x+2y=4代入即可求解;
②利用平方差公式化成式子相乘的形式即可求解.
解:(1)图1中阴影部分面积为a2﹣b2,图2中阴影部分面积为(a+b)(a﹣b),
对照两个图形的面积可以验证平方差公式:a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2,(a+b)(a﹣b),平方差,a2﹣b2=(a+b)(a﹣b).
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),
∴15=3(x﹣2y),
∴x﹣2y=5;
②(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(2﹣1)(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(22﹣1)(22+1)(24+1)(28+1)……(264+1)+1
=(24﹣1)(24+1)(28+1)……(264+1)+1
=(28﹣1)(28+1)……(264+1)+1
=(264﹣1)(264+1)+1
=2128﹣1+1
=2128.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,点C将线段AB分成两部分(AC>BC),如果
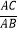 =
= 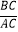 ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果
,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 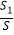 =
= 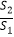 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.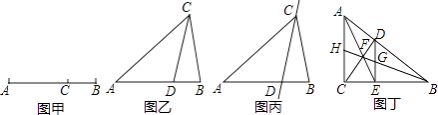
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点A出发,沿AB方向匀速运动,速度为1cm/s;过点P作直线PF∥AD,PF交CD于点F,过点F作EF⊥BD,且与AD、BD分别交于点E、Q;连接PE,设点P的运动时间为t(s)(0<t<10).
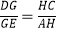 解答下列问题:
解答下列问题:
(1)填空:AB= cm;
(2)当t为何值时,PE∥BD;
(3)设四边形APFE的面积为y(cm2)
①求y与t之间的函数关系式;
②若用S表示图形的面积,则是否存在某一时刻t,使得S四边形APFE=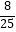 S菱形ABCD?若存在,求出t的值;若不存在,请说明理由.
S菱形ABCD?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AC是⊙O的直径,∠BDC=40°(点D在⊙O上),则∠ACB=( )

A.20°
B.30°
C.40°
D.50° -
科目: 来源: 题型:
查看答案和解析>>【题目】在半径为2cm的⊙O中,弦AB的长为2
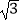 cm,则这条弦所对的圆周角为 .
cm,则这条弦所对的圆周角为 . -
科目: 来源: 题型:
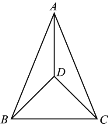
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是三角形内一点,连接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求证:∠BAD=∠CAD;
(2)求∠ADB的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C是线段AB垂直平分线m上一动点,连接AC,以AC为边作等边三角形ACD,点D在直线AB的上方,连接DB与直线m交于点E,连接BC,AE.
(1)如图1,点C在线段AB上.
①根据题意补全图1;
②求证:∠EAC=∠EDC;
(2)如图2,点C在直线AB的上方, 0°<∠CAB<30°,用等式表示线段BE,CE,DE之间的数量关系,并证明.

相关试题

