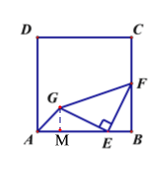
【题目】如图,正方形ABCD 的边长为4,E 为AB 上一点,且AE=3 ,F 为BC 边上的一个动点,连接EF ,以EF 为边向左侧作等腰直角三角形FEG ,EG=EF,∠GEF=90°,连接AG ,则AG 的最小值为________________.

参考答案:
【答案】1
【解析】
过点G作GM⊥AB于点M,由AAS可证:MGE BEF,得GM=1,即:点G与直线AB的距离为1,进而即可得到答案.
过点G作GM⊥AB于点M,
∵以EF 为边向左侧作等腰直角三角形FEG ,EG=EF,∠GEF=90°,
∴∠MGE+∠MEG=∠MEG+∠BEF=90°,
∴∠MGE=∠BEF,
∵正方形ABCD中,∠B=∠GME=90°,
∴MGE BEF(AAS),
∴GM=EB=AB-AE=4-3=1,
∴点G与直线AB的距离为1,
∴当AG⊥AB时,AG 有最小值,最小值为1.
故答案是:1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了1元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2000元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3% 的损耗,第二次购进的水果有4% 的损耗,该水果店希望售完这些水果获利不低于3780元,则该水果每千克售价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,
 ,点E在AD上,且
,点E在AD上,且 ,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A'处,则
,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A'处,则 ____________cm.
____________cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校七(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出如下频数分布表和频数分布直方图:
次数
80≤x<100
100≤x<120
120≤x<140
140≤x<160
160≤x<180
180≤x<200
频数
a
4
12
16
8
3
结合图表完成下列问题:
(1)a= ,全班人数是______;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀学生人数占全班总人数的百分之几?

-
科目: 来源: 题型:
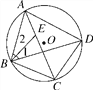
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.
(1)判断BE与⊙O的位置关系,并说明理由;
(2)若∠ACB=30°,⊙O的半径为4,请求出图中阴影部分的面积.

相关试题

