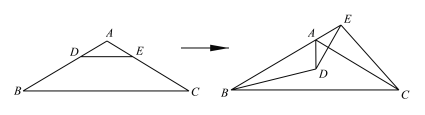
【题目】如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有____________.
参考答案:
【答案】②③④
【解析】
由AB=AC,∠B=30°,得出∠B=∠C=30°,∠BAC=120°,得出将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,△ADE的旋转角为60°,故①错误;由DE∥BC,易证AD=AE,得出BD=EC,故②正确;BE=AE+AB=AD+AC,故③正确;证明∠DAC=∠EAC,由AD=AE,得出DE⊥AC,故④正确;即可得出结果.
解:∵AB=AC,∠B=30°,
∴∠B=∠C=30°,∠BAC=120°,
∴将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,△ADE的旋转角为180°-120°=60°,故①错误;
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠ADE=∠AED,
∴AD=AE,
∴BD=EC,故②正确;
BE=AE+AB=AD+AC,故③正确;
∵∠BAC=∠DAE=120°,
∴∠EAC=180°-∠BAC=180°-120°=60°,∠DAC=120°-∠EAC=120°-60°=60°,
∴∠DAC=∠EAC,
∵AD=AE,
∴DE⊥AC,故④正确;
故答案为:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, 平分
平分 ,点
,点 在射线
在射线 上,
上, 、
、 分别是射线
分别是射线 、
、 上的动点(
上的动点( 、
、 不与点
不与点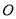 重合),连接
重合),连接 交射线
交射线 于点
于点 .设
.设 .
.
(1)如图1,若
 ,则:①
,则:① ______;②当
______;②当 时,
时, ______
______ .
.(2)如图2,若
 ,垂足为
,垂足为 ,则是否存在这样的
,则是否存在这样的 的值,使得
的值,使得 中存在两个相等的角?若存在,求出
中存在两个相等的角?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC绕点C顺时针旋转得△CEF,当E落在AB边上时,连接BF,取BF的中点D,连接ED,则ED的长是( )
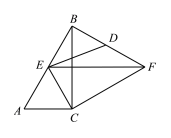
A.2
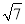 B.4
B.4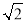 C.6D.4
C.6D.4 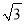
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
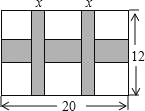
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的
 ,求横、竖彩条的宽度.
,求横、竖彩条的宽度. -
科目: 来源: 题型:
查看答案和解析>>【题目】(操作发现)三角形三个顶点与重心的连线段,将该三角形面积三等分.
(1)如图①:
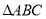 中,中线
中,中线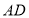 、
、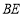 、
、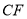 相交于点
相交于点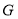 .求证:
.求证: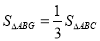 .
.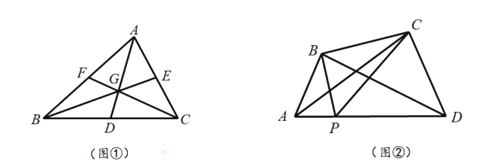
(提出问题)如图②,探究在四边形
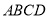 中,
中,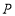 是
是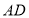 边上任意一点,
边上任意一点,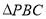 与
与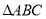 和
和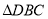 的面积之间的关系.
的面积之间的关系.(2)为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
如图③,当
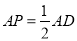 时,探求
时,探求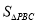 与
与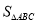 和
和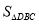 之间的关系,写出求解过程.
之间的关系,写出求解过程.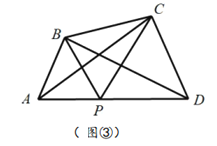
(问题解决)
(3)推广,当
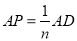 (
(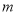 表示正整数)时,直接写出
表示正整数)时,直接写出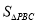 与
与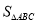 和
和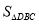 之间的关系:____________.
之间的关系:____________.(4)一般地,当
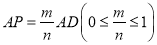 时,
时,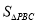 与
与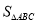 和
和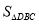 之间的关系式为:____________.
之间的关系式为:____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2
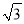 .
.①若∠C=30°,求图中阴影部分的面积;
②若
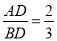 ,求BE的长.
,求BE的长.
相关试题

