【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2![]() .
.
①若∠C=30°,求图中阴影部分的面积;
②若![]() ,求BE的长.
,求BE的长.

参考答案:
【答案】(1)证明见解析;(2)①4![]() -
- ![]() ;②
;②![]() 。
。
【解析】试题分析:(1)首先连接OD,由AB是直径,可得∠ADB=90°,然后由∠CDA=∠CBD,求得∠CDO=90°,即可证得结论;
(2)①由∠CBD=30°,可得△ADO是边长为1的等边三角形,继而求得CD的长,然后由S阴影=S四边形OBED﹣S扇形OBD求得答案;②由∠C=∠C,∠CDA=∠CBD,可证得△CDA∽△CBD,可得比例式![]() =
=![]() ,从而CB=3
,从而CB=3![]() .在直角△CBE中,由勾股定理得到BE的长.
.在直角△CBE中,由勾股定理得到BE的长.
试题解析:(1)连OD.
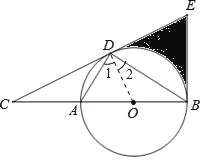
∵AB是直径,
∴∠ADB=90°,即∠ADO+∠2=90°.
又∵∠CDA=∠CBD,∠2=∠CBD,
∴∠2=∠CDA,
∴∠CDA+∠ADO=90°,即∠CDO=90°,
∴CD是⊙O的切线.
(2)①∵BE是⊙O的切线,
∴BE⊥BC.
∵∠C=30°,
∴∠E=60°.
∵DE是⊙O的切线,ED=EB,
∴△EBD是等边三角形,
∴∠EBD=60°,
∴∠DBC=30°,
∴DB=CD=2![]() ,EB=ED=BD=2
,EB=ED=BD=2![]() .
.
在Rt△COD中,∵∠C=30°,CD=2![]() ,
,
∴OD=2.
∴S四边形OBED=2S△BEO=2×![]() ×2×3
×2×3![]() =4
=4![]() .
.
S扇形OBD=![]() =
=![]() ,
,
则S阴影=S四边形OBED﹣S扇形OBD=4![]() ﹣
﹣![]() ;
;
②∵∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CB=3![]() .
.
设BE=ED=x,在直角△CBE中,由勾股定理得到:x2+(3![]() )2=(2
)2=(2![]() +x)2,
+x)2,
解得x=![]() ,所以BE的长为
,所以BE的长为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有____________.
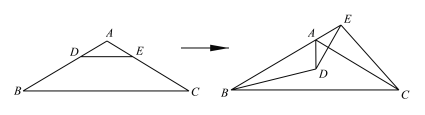
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
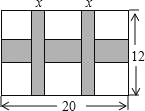
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的
 ,求横、竖彩条的宽度.
,求横、竖彩条的宽度. -
科目: 来源: 题型:
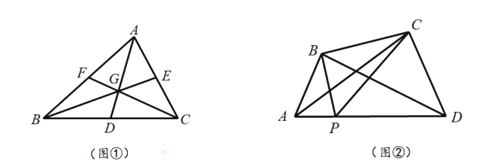
查看答案和解析>>【题目】(操作发现)三角形三个顶点与重心的连线段,将该三角形面积三等分.
(1)如图①:
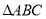 中,中线
中,中线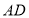 、
、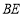 、
、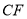 相交于点
相交于点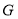 .求证:
.求证: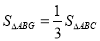 .
.
(提出问题)如图②,探究在四边形
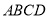 中,
中,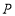 是
是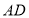 边上任意一点,
边上任意一点,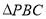 与
与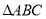 和
和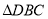 的面积之间的关系.
的面积之间的关系.(2)为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
如图③,当
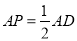 时,探求
时,探求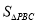 与
与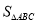 和
和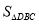 之间的关系,写出求解过程.
之间的关系,写出求解过程.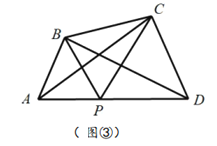
(问题解决)
(3)推广,当
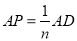 (
(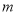 表示正整数)时,直接写出
表示正整数)时,直接写出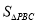 与
与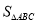 和
和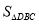 之间的关系:____________.
之间的关系:____________.(4)一般地,当
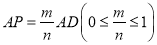 时,
时,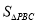 与
与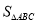 和
和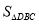 之间的关系式为:____________.
之间的关系式为:____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE.交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,DE的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的三个顶点的坐标分别为A(-3,2)、B(0,4)、C(0,2).
⑴将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C.平移△ABC,若A对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
⑵若将△A1B1C绕某一点旋转得到△A2B2C2,请直接写出旋转中心的坐标为 .
⑶在x轴上找一点P,使得直线CP将△ABC的面积分为1:2,直接写出P点的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=
 x+
x+ 与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).
与y轴的交点为A,直线l1与直线l2:y=kx的交点M的坐标为M(3,a).⑴a= ,k= ;
⑵直接写出关于x的不等式
 x+
x+ ≥kx>0的解集 ;
≥kx>0的解集 ;⑶若点B在x轴上,MB=MA,直接写出点B的坐标 .
⑷在x轴上是否存在一点N,使得NM-NA的值最大,若不存在,请说明理由;若存在,请直接写出点N的坐标.

相关试题

