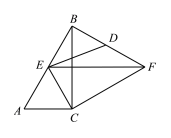
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=4,△ABC绕点C顺时针旋转得△CEF,当E落在AB边上时,连接BF,取BF的中点D,连接ED,则ED的长是( )
A.2![]() B.4
B.4![]() C.6D.4
C.6D.4 ![]()
参考答案:
【答案】A
【解析】
先证明△ACE,△BCF是等边三角形,可求BD,BE的长,由勾股定理可求解.
解:∵∠ACB=90°,∠ABC=30°,AC=4,
∴∠A=90°![]() ∠ABC=60°,AB=8,BC=
∠ABC=60°,AB=8,BC=![]() ,
,
∵△ABC绕点C顺时针旋转得△CEF,
∴CA=CE,∠ACE=∠BCF,BC=CF,
∴△ACE是等边三角形,AE=AC=BE=EC=4,
∴∠BCF=∠ACE=60°,
∵CB=CF,
∴△BCF是等边三角形,
∴BF=BC=![]() ,∠CBF=60°,
,∠CBF=60°,
∵点D是BF中点,
∴BD=![]() ,且BE=4,∠ABF=90°,
,且BE=4,∠ABF=90°,
∴DE=![]() ;
;
故选:A.
-
科目: 来源: 题型:
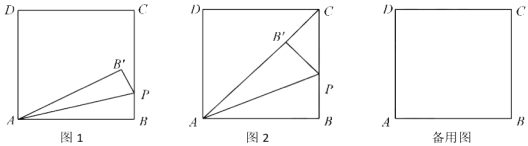
查看答案和解析>>【题目】如图1,在矩形
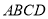 中,BC=3,动点
中,BC=3,动点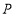 从
从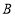 出发,以每秒1个单位的速度,沿射线
出发,以每秒1个单位的速度,沿射线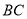 方向移动,作
方向移动,作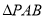 关于直线
关于直线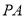 的对称
的对称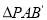 ,设点
,设点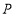 的运动时间为
的运动时间为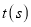
(1)若
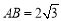
①如图2,当点B’落在AC上时,显然△PCB’是直角三角形,求此时t的值
②是否存在异于图2的时刻,使得△PCB’是直角三角形?若存在,请直接写出所有符合题意的t的值?若不存在,请说明理由
(2)当P点不与C点重合时,若直线PB’与直线CD相交于点M,且当t<3时存在某一时刻有结论∠PAM=45°成立,试探究:对于t>3的任意时刻,结论∠PAM=45°是否总是成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂准备用图甲所示的
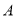 型正方形板材和
型正方形板材和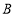 型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.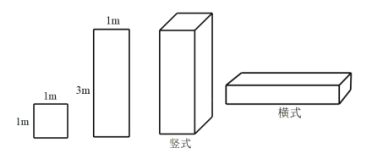
(1)若该工厂准备用不超过2400元的资金去购买
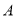 ,
,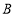 两种型号板材,制作竖式、横式箱子共10个,已知
两种型号板材,制作竖式、横式箱子共10个,已知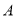 型板材每张20元,
型板材每张20元,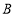 型板材每张60元,问最多可以制作竖式箱子多少只?
型板材每张60元,问最多可以制作竖式箱子多少只?(2)若该工程新购得65张规格为
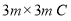 型正方形板材,将其全部切割测好难过
型正方形板材,将其全部切割测好难过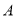 型或
型或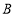 型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只.
型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10只,且材料恰好用完,则能制作竖式箱子______只. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 ,
, 平分
平分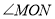 ,点
,点 在射线
在射线 上,
上, 、
、 分别是射线
分别是射线 、
、 上的动点(
上的动点( 、
、 不与点
不与点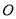 重合),连接
重合),连接 交射线
交射线 于点
于点 .设
.设 .
.
(1)如图1,若
 ,则:①
,则:① ______;②当
______;②当 时,
时, ______
______ .
.(2)如图2,若
 ,垂足为
,垂足为 ,则是否存在这样的
,则是否存在这样的 的值,使得
的值,使得 中存在两个相等的角?若存在,求出
中存在两个相等的角?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+3.
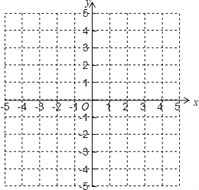
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
-
科目: 来源: 题型:
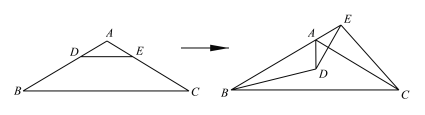
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确的有____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
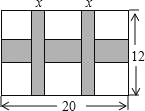
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的
 ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
相关试题

