【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为( )

A. 16B. 32C. 64D. 128
参考答案:
【答案】B
【解析】
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2…进而得出答案.
∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,

∴∠2=120°,
∵∠MON=30°,
∴∠1=180°120°30°=30°,
又∵∠3=60°,
∴∠5=180°60°30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,
∴A3B3=4B1A2=4,A4B4=8B1A2=8,A5B5=16B1A2=16,
以此类推:△AnBnAn+1的边长为2n-1,
∴△A6B6A7的边长为:26-1=32.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
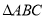 和
和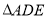 中,
中,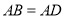 ,
, ,
,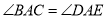 ,
, 交
交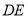 于点
于点 ,
,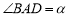 .
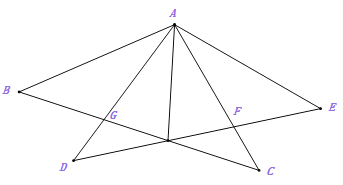
.(1)如图1,求证:
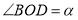 ;
;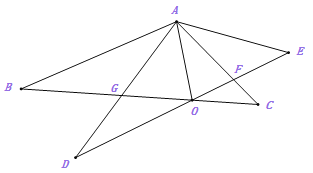
(2)如图2,若
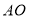 平分
平分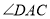 ,求证:
,求证: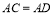 ;
;
(3)若
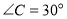 ,
,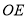 交
交 于
于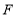 ,且
,且 为等腰三角形,则
为等腰三角形,则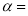 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=
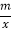 的图象交于A(2,3),B(6,n)两点.
的图象交于A(2,3),B(6,n)两点.(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
 交
交 轴于
轴于 点,交
点,交 轴于
轴于 点,且
点,且 .点
.点 是线段
是线段 上一点,
上一点, 交
交 的延长线于点
的延长线于点 .
.(1)如图1,若
 交
交 于点
于点 .点
.点 作
作 ,交
,交 的延长线于点
的延长线于点 ,求证:
,求证: ;
;
(2)如图2,若
 是
是 的角平分线,
的角平分线, 交
交 于点
于点 ,交
,交 于点
于点 ,求
,求 的值;
的值;
(3)如图3,若
 交
交 的延长线于点
的延长线于点 .请证明:
.请证明: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步促进“美丽校园”创建工作,某校团委计划对八年级五个班的文化建设进行检查,每天随机抽查一个班级,第一天从五个班级随机抽取一个进行检查,第二天从剩余的四个班级再随机抽取一个进行检查,第三天从剩余的三个班级再随机抽取一个进行检查…,以此类推,直到检查完五个班级为止,且每个班级被选中的机会均等
(1)第一天,八(1)班没有被选中的概率是 ;
(2)利用网状图或列表的方法,求前两天八(1)班被选中的概率
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,他们的运动时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由
(2)判断此时线段PC和线段PQ的关系,并说明理由。
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变,设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC为⊙O的直径,点D在⊙O上,连结BD、CD,过点D的切线AE与CB的延长线交于点A,∠BCD=∠AEO,OE与CD交于点F.
(1)求证:OF∥BD;
(2)当⊙O的半径为10,sin∠ADB=
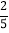 时,求EF的长.
时,求EF的长.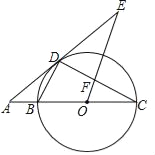
相关试题

