【题目】如图,在ABCD中,过点D作DE⊥BD交BA的延长线于点E.
(1)当ABCD是菱形时,证明:AE=AB;
(2)当ABCD是矩形时,设∠E=α,问:∠E与∠DOA满足什么数量关系?写出结论并说明理由.

参考答案:
【答案】(1)证明见解析;(2)∠E=90°﹣![]()
【解析】
(1)由四边形ABCD是菱形可得AC⊥BD,AB=CD,根据DE⊥BD,可证四边形ACDE是平行四边形,可证得结论.(2)由题意可得∠DOA=2∠OBA,∠E=90°-∠OBA,即可求∠E与∠DOA的数量关系.
证明:(1)∵四边形ABCD是菱形,
∴AC⊥BD,AB∥CD,AB=CD;
∵DE⊥BD,AC⊥BD,
∴AC∥DE,且CD∥AB,
∴四边形ACDE是平行四边形,
∴AE=CD且AB=CD,
∴AE=AB;
(2)∠E=90°﹣![]() ,
,
∵四边形ABCD是矩形,
∴AO=BO,
∴∠OBA=∠OAB;
∵DE⊥BD,∠DOA=∠OBA+∠OAB,
∴∠E=90°﹣∠OBA,∠DOA=2∠OBA,
∴∠E=90°﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).

①请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;
②请画出△ABC绕点B逆时针旋转90°后的△A2BC2 , 并写出点A2、C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)已知∠DAB=60°,AF是∠DAB的平分线,若AD=3,求DC的长度.

-
科目: 来源: 题型:
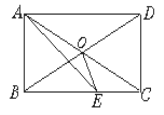
查看答案和解析>>【题目】如图,在矩形ABCD中,AC、BD相交于O,AE平分∠BAD,交BC于E,若∠CAE=15°,求∠BOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时)
挖掘土石方量(单位:m3/台时)
甲型挖掘机
100
60
乙型挖掘机
120
80
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+3x+
 =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为符合条件的最大整数,求此时方程的根. -
科目: 来源: 题型:
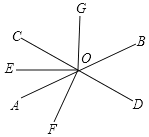
查看答案和解析>>【题目】如图,直线AB与CD相交于O,OE是∠AOC的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOC,∠AOF的度数;
(2)求∠EOF与∠BOG是否相等?请说明理由.
相关试题

