搜索
【题目】已知点A(8，0)及在第四象限的动点P(x，y)，且x＋y＝10，设△OPA的面积为S
(1) 求S关于x的函数表达式，并直接写出x的取值范围
(2) 画出函数S的图象
(3) S＝12时，点P坐标为
参考答案：
【答案】（1）S＝404x（0＜x＜10）；（2）见解析；（3）（7，3）.
【解析】
（1）首先把x＋y＝10，变形成y＝10x，再利用三角形的面积求法可以得到S关于x的函数表达式；P在第一象限，故x＞0，再利用三角形的面积S＞0，可得到x的取值范围；
（2）根据函数解析式描点，画图，注意x，y的范围．
（3）把S＝12代入函数解析式即可；
解：（1）∵x＋y＝10
∴y＝10x，
∴S＝8（10x）÷2＝404x，
∵404x＞0，
∴x＜10，
∴x的取值范围是：0＜x＜10，即S＝404x（0＜x＜10）；
（2）函数S的图象如图所示：
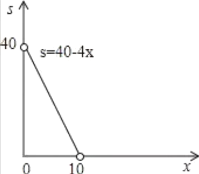
（3）∵S＝12，
∴12＝404x，
∴x＝7，
∴y＝107＝3，
∴s＝12时，P点坐标（7，3）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线l
经过A（2，3）B（
，0）
(1) 求直线l
的解析式及l与坐标轴围成的图形的面积.(2) 将l
向下平移3个单位长度，再向左平移1个单位长度，得到直线l
，画出l的图象并直接写出l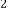的解析式__________________.(3)若点M（
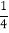，m），N（n，1）在直线l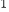上，P为y轴上一动点，则PM+PN最小时，P的坐标为____________，此时PM+PN=______________. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系
中，点
的坐标为(0，4)，线段
的位置如图所示，其中点
的坐标为(
，
)，点
的坐标为(3，
).
(1)将线段
平移得到线段
，其中点的对应点为，点的对应点为点
.①点
平移到点的过程可以是：先向 平移 个单位长度，再向 平移 个单位长度；②点
的坐标为 .(2)在(1)的条件下，若点
的坐标为(4，0)，连接
，画出图形并求
的面积. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知一块四边形的草地ABCD，其中∠B＝90°，AB＝20m，BC＝15m，CD＝7m，DA＝24m，求这块草地的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市举行“第十七届中小学生书法大赛”作品比赛，已知每幅参赛作品成绩记为
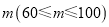，组委会从1000幅书法作品中随机抽取了部分参赛作品，统计了它们的成绩，并绘制成如下统计图表.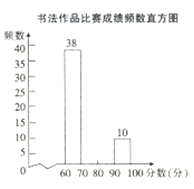
分数段
频数
百分比
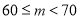
38
0.38
______
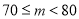
0.32
______
______
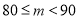
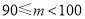
10
0.1
合计
______
1
根据上述信息，解答下列问题：
(1)请你把表中的数据填写完整.
(2)补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖，试估计全市获得等级奖的幅数.
-
科目： 来源： 题型：
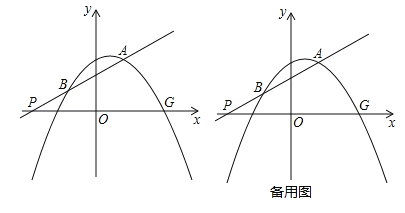
查看答案和解析>>【题目】如图，二次函数y=﹣
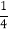x2+mx+n的图象经过点A（2，3），与x轴的正半轴交于点G（1+
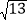，0）；一次函数y=kx+b的图象经过点A，且交x轴于点P，交抛物线于另一点B，又知点A，B位于点P的同侧．（1）求这个二次函数的解析式；
（2）若PA=3PB，求一次函数的解析式；
（3）在（2）的条件下，当k＞0时，抛物线的对称轴上是否存在点C，使⊙C同时与x轴和直线AP都相切？如果存在，请求出点C的坐标；如果不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法错误的有（ ）
①有理数包括正有理数和负有理数； ②绝对值等于它本身的数是非负数；③若|b|=|﹣5|，则b=-5 ； ④当b=2时，5﹣|2b﹣4|有最小值是5；⑤若
、
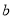互为相反数，则
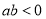；⑥
是关于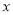
、
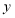的六次三项式.A.2个B.3个C.4个D.5个
相关试题
