【题目】根据要求回答问题:
(1)发现
如图1,直线l1∥l2 , l1和l2的距离为d,点P在l1上,点Q在l2上,连接PQ,填空:PQ长度的最小值为.
(2)应用
如图2,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M在线段AD上,AM=3MD,点N在直线BC上,连接MN,求MN长度的最小值
(3)拓展
如图3,在四边形ABCD中,DC∥AB,AD⊥AB,DC=2,AD=4,AB=6,点M在线段AD上任意一点,连接MC并延长到点E,使MC=CE,以MB和ME为边作平行四边形MBNE,请直接写出线段MN长度的最小值
参考答案:
【答案】
(1)d
(2)解:如图2,

∵AD=4,AM=3DM,
∴AM=3,DM=1,
延长AD、BC交于E,
当MN⊥BC时,MN的值最小,
∵DC∥AB,
∴△EDC∽△EAB,
∴ ![]() ,
,
∴ ![]() ,
,
∴ED=2,
∴ED=DC=2,
∴△EDC是等腰直角三角形,
∴∠E=45°,
∴△EMN是等腰直角三角形,
∵EM=3,
∴MN= ![]() =
= ![]()
(3)解:当MN⊥AD时,MN的长最小,
∴MN∥DC∥AB,
∴∠DCM=∠CMN=∠MNB=∠NBH,
设MN与BC相交于点G,
∵ME∥BN,MC=CE,
∴ ![]() ,
,
∴G是BC上一定点,
作NH⊥AB,交AB的延长线于H,

∵∠D=∠H=90°,
∴Rt△MDC∽Rt△NHB,
即 ![]() =
= ![]() ,
,
∴BH=2DC=4,
∴AH=AB+BH=6+4=10,
∴当MN⊥AD时,MN的长最小,即为10;
则线段MN长度的最小值为10
【解析】解:(1)∵直线l1∥l2,l1和l2的距离为d,
∴PQ长度的最小值为d;
所以答案是:d;
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )

A. a+b<0 B. a-b<0
C. -a<-b D. |a-b|=b-a
-
科目: 来源: 题型:
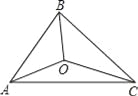
查看答案和解析>>【题目】如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法:①方程x2-3x+2=0是“倍根方程”;②若(x-2)(mx+n)=0是“倍根方程”,则4m2+5mn+n2=0;③若pq=2,则关于x的方程px2+3x+q=0是“倍根方程”;④若方程ax2+bx+c=0是“倍根方程”,且5a+b=0,则方程ax2+bx+c=0的一个根为
 .其中正确的是____(填序号).
.其中正确的是____(填序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,其中点A在y轴的左侧,点C在x轴的下方,且OA=OC=5.
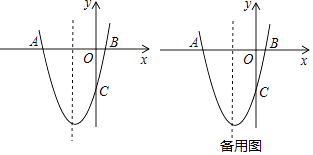
(1)求抛物线对应的函数解析式;
(2)点P为抛物线对称轴上的一动点,当PB+PC的值最小时,求点P的坐标;
(3)在(2)条件下,点E为抛物线的对称轴上的动点,点F为抛物线上的动点,以点P、E、F为顶点作四边形PEFM,当四边形PEFM为正方形时,请直接写出坐标为整数的点M的坐标. -
科目: 来源: 题型:
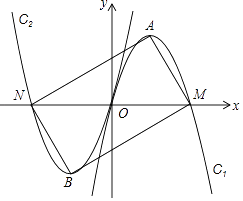
查看答案和解析>>【题目】如图,经过坐标原点的抛物线C1:y=ax2+bx与x轴的另一交点为M,它的顶点为点A,将C1绕原点旋转180°,得到抛物线C2 , C2与x轴的另一交点为N,顶点为点B,连接AM,MB,BN,NA,当四边形AMBN恰好是矩形时,则b的值( )
A.2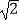
B.﹣2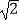
C.2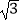
D.﹣2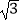
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )

A.
 B.
B.  C.
C.  D.
D. 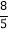
相关试题

