【题目】如图,已知∠DAE=∠B,∠DAB=∠C,则下列结论不成立的是( )
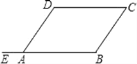
A.AD∥BCB.AB∥CDC.∠DAB+∠B=180°D.∠B=∠C
参考答案:
【答案】D
【解析】
由∠DAE=∠B依据“同位角相等,两直线平行”即可得出AD∥BC即A成立;依据“两直线平行,同旁内角互补”可得出∠DAB+∠B=180°,即C成立;由等量替换即可得出∠B+∠C=180°,即B成立;无法判断D是否成立.由此即可得出结论.
解:A.∵∠DAE=∠B,
∴AD∥BC,故A成立;
C.∵AD∥BC,
∴∠DAB+∠B=180°,
∵∠DAB=∠C,
∴∠B+∠C=180°,故C成立;
B.∵∠B+∠C=180°,
∴AB//CD,故B成立;
D.无法证明∠B=∠C,故D不成立;
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A.
(1)当x取何值时y1>y2?
(2)当直线BA平分△BOC的面积时,求点A的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是△ABC边BC上一点,AD=BD,且AD平分∠BAC.(1)若∠B=50°,求∠ADC的度数;(2)若∠C=30°,求∠ADC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:
 .
.(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,分别过B,C向经过点A的直线EF作垂线,垂足为E,F.
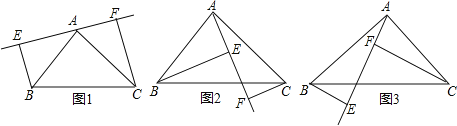
(1)如图1,当EF与斜边BC不相交时,请证明EF=BE+CF;
(2)如图2,当EF与斜边BC相交时,其他条件不变,写出EF、BE、CF之间的数量关系,并说明理由;
(3)如图3,猜想EF、BE、CF之间又存在怎样的数量关系,写出猜想,不必说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A,B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
相关试题

