【题目】如图,点D是△ABC边BC上一点,AD=BD,且AD平分∠BAC.(1)若∠B=50°,求∠ADC的度数;(2)若∠C=30°,求∠ADC的度数.

参考答案:
【答案】(1)100°;(2)100°.
【解析】试题分析:(1)由AD=BD可得∠B=∠BAD=50°,进而得出∠ADC=∠B+∠BAD=100°;(2)设∠B=∠BAD=x,则∠ADC=2x,由AD平分∠BAC可得∠BAD=∠DAC=x,又因为∠C=30°,故根据三角形内角和为180°可列方程x+2x+30=180,解得x=50,所以∠ADC=100°.
试题解析:
(1)∵AD=BD,
∴∠B=∠BAD=50°,
∴∠ADC=∠B+∠BAD=100°;
(2)设∠B=∠BAD=x,则∠ADC=2x,
∵AD平分∠BAC,
∴∠BAD=∠DAC=x,
∵∠C=30°,
∴x+2x+30=180,解得x=50,
∴∠ADC=100°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组在研究函数y=
 x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.x
…
﹣4
﹣3.5
﹣3
﹣2
﹣1
0
1
2
3
3.5
4
…
y
…
﹣

﹣




0
﹣

﹣

﹣


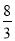
…
(1)请补全函数图象;
(2)方程
 x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;(3)观察图象,写出该函数的两条性质.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
(1)等边三角形“內似线”的条数为 ;
(2)如图,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“內似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别在边AC、BC上,且EF是△ABC的“內似线”,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习“有理数加法“时,我们利用“(+5)+(+3)=+8,(-5)+(-3)=-8,……”抽象归纳推出了“同号两数相加,取相同的符号,并把绝对值相加”的加法法则.这种推导方法叫( )
A.排除法B.归纳法C.类比法D.数形结合法
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将550000用科学记数法表示是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大于-2且小于3的所有整数的和为_________.
相关试题

