【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
参考答案:
【答案】A
【解析】
过两把直尺的交点C作CF⊥BO与点F,由题意得CE⊥AO,因为是两把完全相同的长方形直尺,可得CE=CF,再根据角的内部到角的两边的距离相等的点在这个角的平分线上可得OP平分∠AOB
如图所示:过两把直尺的交点C作CF⊥BO与点F,由题意得CE⊥AO,
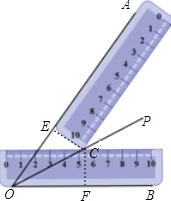
∵两把完全相同的长方形直尺,
∴CE=CF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习了正方形后,数学小组的同学对正方形进行了探究,发现:
(1)如图1,在正方形ABCD中,点E为BC边上任意一点(点E不与B、C重合),点F在线段AE上,过点F的直线MN⊥AE,分别交AB、CD于点M、N . 此时,有结论AE=MN,请进行证明;
(2)如图2:当点F为AE中点时,其他条件不变,连接正方形的对角线BD, MN 与BD交于点G,连接BF,此时有结论:BF= FG,请利用图2做出证明.
(3)如图3:当点E为直线BC上的动点时,如果(2)中的其他条件不变,直线MN分别交直线AB、CD于点M、N,请你直接写出线段AE与MN之间的数量关系、线段BF与FG之间的数量关系.

图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点顺时针方向旋转180°后得到四边形A1B1C1D1 .

(1)写出点D1的坐标;
(2)将四边形A1B1C1D1平移,得到四边形A2B2C2D2 , 若点D2(4,5),画出平移后的图形;
(3)求点D旋转到点D1所经过的路线长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
(1)甲出发几小时,乙才开始出发?
(2)乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
(3)甲从下午2时到5时的速度是多少?
(4)乙行驶的速度是多少?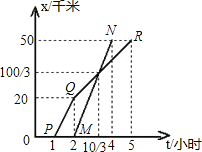
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二维码已经给我们的生活带来了很大方便,它是由大小相同的黑白两色的小正方形(如图中C型黑白一样)按某种规律组成的一个大正方形。现有25×25格式的正方形如图,角上是三个7×7的A型大黑白相间正方形,中间右下有一个5×5的B型黑白相间正方形((A,B型均由C型黑白两色小正方形组成),除这4个正方形外,其他的C型小正方形黑色块数正好是白色块数的3倍多53块,则该25×25格式的二维码中除去A、B型后,有__块C型白色小正方形,整个二维码中共有__块C型白色小正方形.

相关试题

