【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1: ![]() ,则大楼AB的高度约为( )(精确到0.1米,参考数据:
,则大楼AB的高度约为( )(精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,
≈1.73, ![]() ≈2.45)
≈2.45)
A.30.6
B.32.1
C.37.9
D.39.4
参考答案:
【答案】D
【解析】解:延长AB交DC于H,作EG⊥AB于G,如图所示: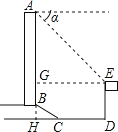
则GH=DE=15米,EG=DH,
∵梯坎坡度i=1: ![]() ,
,
∴BH:CH=1: ![]() ,设BH=x米,则CH=
,设BH=x米,则CH= ![]() x米,
x米,
在Rt△BCH中,BC=12米,
由勾股定理得:x2+( ![]() x)2=122 , 解得:x=6,
x)2=122 , 解得:x=6,
∴BH=6米,CH=6 ![]() 米,
米,
∴BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=6 ![]() +20(米),
+20(米),
∵∠α=45°,
∴∠EAG=90°﹣45°=45°,
∴△AEG是等腰直角三角形,
∴AG=EG=6 ![]() +20(米),
+20(米),
∴AB=AG+BG=6 ![]() +20+9≈39.4(米);
+20+9≈39.4(米);
故选:D.
【考点精析】根据题目的已知条件,利用关于坡度坡角问题的相关知识可以得到问题的答案,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(﹣2,0)、B(4,0),其顶点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.

(1)求抛物线的解析式,并写出顶点D的坐标;
(2)设P点的坐标为(x,y),△PBE的面积为S,求S与x之间的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取值最大值时,过点P作x轴的垂线,垂足为F,连接EF,△PEF沿直线EF折叠,点P的对应点为点P′,请直接写出P′点的坐标,并判断点P′是否在该抛物线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是( )

A.43
B.45
C.51
D.53 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )

A.18 ﹣9π
﹣9π
B.18﹣3π
C.9 ﹣
﹣ 
D.18 ﹣3π
﹣3π -
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的分式方程
 ﹣3=
﹣3=  有负分数解,且关于x的不等式组
有负分数解,且关于x的不等式组  的解集为x<﹣2,那么符合条件的所有整数a的积是( )
的解集为x<﹣2,那么符合条件的所有整数a的积是( )
A.﹣3
B.0
C.3
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】点P的坐标是(a,b),从﹣2,﹣1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第秒.

相关试题

