搜索
【题目】在平面直角坐标系中, △ABC的三个顶点的位置如图所示，点A'的坐标是
（－2,2）, 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。
（1）请画出平移后的像△A'B'C'（不写画法) ，并直接写出点B′、C′的坐标:
B′ （ ） 、C′ （ ） ；
（2）若△ABC 内部一点P的坐标为（a,b），则点P 的对应点P ′的坐标是 （ ） .
参考答案：
【答案】(1)请画出平移后的像△A'B'C' ，B′（ －4，1 ） 、C′（ -1，-1 ） ；
（2）P ′的坐标是 （a-5,b-2）
【解析】（1）如图，△A′B′C′即为所求，点B′的坐标为（－4，1），点C′的坐标为（－1，－1）．
（2）依据题意点P也应先向左平移5个单位长度，再向下平移2个单位长度，故点P′的坐标应为（a－5，b－2）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2（m+1）x+m2+2=0
（1）若方程有实数根，求实数m的取值范围；
（2）若方程两实数根分别为x1、x2，且满足x12+x22=10，求实数m的值．
-
科目： 来源： 题型：
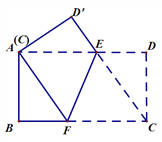
查看答案和解析>>【题目】如图，将矩形ABCD折叠，使C点与A点重合，折痕为EF.
（1）判断四边形AFCE的形状，并说明理由；
（2）若AB=4，BC=8，求折痕EF的长.
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们已经知道(a﹣b)2≥0，即a2﹣2ab+b2≥0．所以a2+b2≥2ab(当且仅当a=b时取等号)．
阅读1：若a、b为实数，且a＞0，b＞0．
∵(
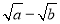)2≥0，∴a﹣2
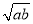+b≥0，∴a+b≥2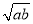(当且仅当a=b时取等号)．阅读2：若函数y=x
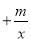(m＞0，x＞0，m为常数)．由阅读1结论可知：x
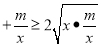即x
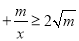∴当x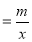
即x2=m，∴x=
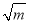(m＞0)时，函数y=x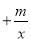的最小值为2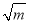．阅读理解上述内容，解答下列问题：
问题1：当x＞0时，
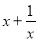的最小值为 ；当x＜0时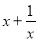，的最大值为 ．问题2：函数y=a+
(a＞1)的最小值为 ．问题3：求代数式
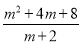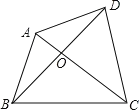
(m＞﹣2)的最小值，并求出此时的m的值．问题4：如图，四边形ABCD的对角线AC，BD相交于点O，△AOB、△COD的面积分别为4和16，求四边形ABCD面积的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】四边形ABCD中，AD∥BC，要判别四边形ABCD是平行四边形，还需满足条件（ ）
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB＝60°，∠CAB＝45°，BC＝4，点D为AB边上一个动点，连接CD，以DA、DC为一组邻边作平行四边形ADCE，则对角线DE的最小值是（ ）
A.
+
B.1+
C.4D.2+2 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，AB∥CD，∠ABC＝90°，AD＝CD+AB，∠BAC＝45°，E是BC上一点，且∠DAE＝45°，若BC＝8，则△ADE面积为__．
相关试题
