【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=90°,AD=CD+AB,∠BAC=45°,E是BC上一点,且∠DAE=45°,若BC=8,则△ADE面积为__.

参考答案:
【答案】![]()
【解析】
过点A作CD的垂线,交CD的延长线于点F,可得四边形ABCF是正方形,设CD=m,根据勾股定理可求出m=2,将△ABE绕点A顺时针旋转90°至△AFG,可以证明△ADE≌△ADG,设BE=n,再根据勾股定理可求DG的长,进而可得△ADG的面积,即可得△ADE的面积.
解:如图,过点A作CD的垂线,交CD的延长线于点F,

![]() ,
,
![]() ,
,
![]() .
.
![]()
∴四边形ABCF是矩形.
∵∠ABC=90°,∠BAC=45°,
∴AB=BC,
∴四边形ABCF是正方形,
∴AB=BC=AF=CF=8,
设CD=m,
则AD=CD+AB=m+8,DF=CF﹣CD=8﹣m,
在Rt△AFD中,根据勾股定理,得
(m+8)2=(8﹣m)2+82,
解得m=2,
∴FD=6,AD=10,
将△ABE绕点A顺时针旋转90°至△AFG,
∴AG=AE,BE=FG,∠EAG=∠BAF=90°,
∵∠BAC=45°,∠DAE=45°,
∴∠BAE=∠DAC,
∴∠CAE=∠DAF,
∵∠BAE=∠FAG,
∴∠DAE=∠DAG,
AD=AD,
∴△ADE≌△ADG(SAS),
∴DE=DG,
设BE=n,则CE=BC﹣BE=8﹣n,DE=DG=DF+FG=DF+BE=6+n,
在Rt△DCE中,根据勾股定理,得
(6+n)2=(8﹣n)2+22
解得n=![]() ,
,
∴DG=6+![]() =
=![]() ,
,
∴S△ADE=S△ADG=![]() DG×AF=
DG×AF=![]() ×8=
×8=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。

(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 ( ) .
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AD∥BC,要判别四边形ABCD是平行四边形,还需满足条件( )
A. ∠A+∠C=180°B. ∠B+∠D=180°
C. ∠A+∠B=180°D. ∠A+∠D=180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=60°,∠CAB=45°,BC=4,点D为AB边上一个动点,连接CD,以DA、DC为一组邻边作平行四边形ADCE,则对角线DE的最小值是( )

A.
 +
+ B.1+
B.1+ C.4D.2+2
C.4D.2+2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是等边三角形ABC的高,点E是AD上的一个动点(点E不与点A重合),连接CE,将线段CE绕点E顺时针旋转60°得到EF,连接BF、CF.
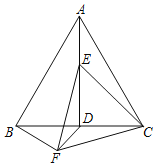
(1)猜想:△CEF是 三角形;
(2)求证:AE=BF;
(3)若AB=4,连接DF,在点E运动的过程中,请直接写出DF的最小值 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.

(1)求y与x之间的函数关系式;
(2)老张种植柑橘的成本是800元/吨,当客商采购量是多少时,老张在这次销售柑橘时获利最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
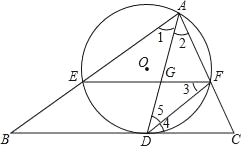
相关试题

