【题目】已知关于x的一元二次方程x2﹣2(m+1)x+m2+2=0
(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1、x2,且满足x12+x22=10,求实数m的值.
参考答案:
【答案】(1)m≥![]() (2)实数m的值为1.
(2)实数m的值为1.
【解析】试题分析:(1)根据方程的系数结合根的判别式即可得出关于m的一元一次不等式,解之即可得出结论;
(2)根据根与系数的关系即可得出x1+x2=2(m+1)、x1x2=m2+2,结合x12+x22=10即可得出关于m的一元二次方程,解之即可得出m的值,再结合(1)的结论即可得出结论.
试题解析:(1)∵方程x2﹣2(m+1)x+m2+2=0有实数根,
∴△=[﹣2(m+1)]2﹣4(m2+2)=8m﹣4≥0,
解得:m≥![]() .
.
(2)∵方程x2﹣2(m+1)x+m2+2=0的两实数根分别为x1、x2,
∴x1+x2=2(m+1),x1x2=m2+2,
∴x12+x22=(x1+x2)2﹣2x1x2=[2(m+1)]2﹣2(m2+2)=2m2+8m=10,
解得:m1=﹣5(舍去),m2=1.
∴实数m的值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,AO=AB,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′、B′在x轴上.则点B'的坐标是______

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次根式中也有这种相辅相成的“对子”.如:
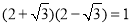 ,
,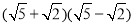 =3,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样理解:如:
=3,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样理解:如: ,
,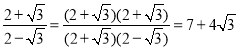 .像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
.像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.解决问题:
(1)3-
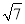 的有理化因式是_________,
的有理化因式是_________,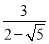 的分母有理化得__________;
的分母有理化得__________;(2)计算:
①已知:
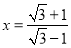 ,
,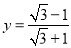 ,求
,求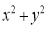 的值;
的值;②
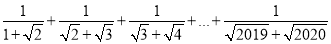 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(用方程解决问题)新冠疫情期间,N95口罩每只的进价比一次性医用口罩每只进价多10元,某药店分别花20000元和60000元购进一次性医用口罩和N95口罩,购进的一次性医用口罩的数量是N95口罩数量的2倍.
(1)求N95口罩进价每只多少元?
(2)国家规定:N95口罩销售价不得高于30元/只.根据市场调研:N95口罩每天的销量y(只)与销售单价x(元/只)之间的函数关系式为y=-10x+500,该药店决定对一次性医用口罩按进价销售,但又想销售口罩每天获利2400元,该药店需将N95口罩的销售价格定为每只多少元?
-
科目: 来源: 题型:
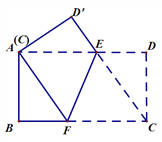
查看答案和解析>>【题目】如图,将矩形ABCD折叠,使C点与A点重合,折痕为EF.
(1)判断四边形AFCE的形状,并说明理由;
(2)若AB=4,BC=8,求折痕EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们已经知道(a﹣b)2≥0,即a2﹣2ab+b2≥0.所以a2+b2≥2ab(当且仅当a=b时取等号).
阅读1:若a、b为实数,且a>0,b>0.
∵(
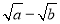 )2≥0,∴a﹣2
)2≥0,∴a﹣2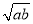 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2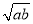 (当且仅当a=b时取等号).
(当且仅当a=b时取等号).阅读2:若函数y=x
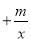 (m>0,x>0,m为常数).由阅读1结论可知:x
(m>0,x>0,m为常数).由阅读1结论可知:x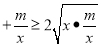 即x
即x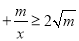 ∴当x
∴当x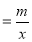 即x2=m,∴x=
即x2=m,∴x=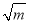 (m>0)时,函数y=x
(m>0)时,函数y=x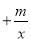 的最小值为2
的最小值为2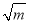 .
.阅读理解上述内容,解答下列问题:
问题1:当x>0时,
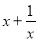 的最小值为 ;当x<0时,
的最小值为 ;当x<0时,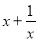 的最大值为 .
的最大值为 .问题2:函数y=a+
 (a>1)的最小值为 .
(a>1)的最小值为 .问题3:求代数式
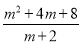 (m>﹣2)的最小值,并求出此时的m的值.
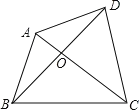
(m>﹣2)的最小值,并求出此时的m的值.问题4:如图,四边形ABCD的对角线AC,BD相交于点O,△AOB、△COD的面积分别为4和16,求四边形ABCD面积的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。

(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 ( ) .
相关试题

