【题目】综合题
(1)【结论再现】如图①,在 ![]() 中,
中, ![]() ,
, ![]() ,则
,则 ![]()
![]() ,
, ![]() .
. 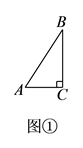
(2)【问题解决】
如图②,四边形 ![]() 是一张边长为
是一张边长为 ![]() 的正方形纸片,
的正方形纸片, ![]() 、
、 ![]() 分别为
分别为 ![]() 、
、 ![]() 的中点,沿过点
的中点,沿过点 ![]() 的折痕将纸片翻折,使点
的折痕将纸片翻折,使点 ![]() 落在
落在 ![]() 上的点
上的点 ![]() 处,折痕交
处,折痕交 ![]() 于点
于点 ![]() ,求
,求 ![]() 的度数和
的度数和 ![]() 的长.
的长.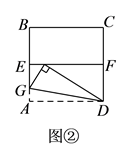
(3)【问题探究】
如图③,点 ![]() 是等腰
是等腰 ![]() 斜边
斜边 ![]() 所在直线上一点,且满足
所在直线上一点,且满足 ![]() ,求
,求 ![]() 的大小和此时
的大小和此时 ![]() 的值.
的值.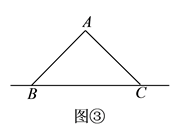
参考答案:
【答案】
(1)解: ![]() ,
,![]()
(2)解:∵ ![]() 折叠后得到
折叠后得到 ![]() ,
,
∴ ![]() ,且
,且 ![]() ,
,
∴在 ![]() 中,
中, ![]() ,sin∠FA′D=
,sin∠FA′D= ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
在 ![]() 中,
中, ![]() ,
,
∴ ![]() ,
,
又∵在 ![]() 中,
中, ![]() ,那么
,那么 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
则 ![]() ,
,
那么 ![]()
![]()
![]()
(3)解:如图,
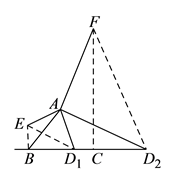
①当 ![]() 在
在 ![]() 边上时,将线段
边上时,将线段 ![]() 绕点
绕点 ![]() 顺时针方向旋转
顺时针方向旋转 ![]() 得到线段
得到线段 ![]() ,连接
,连接 ![]() ,
,
与(1)同理可证 ![]() ≌
≌ ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴四边形 ![]() .
. ![]() 、
、 ![]() .
. ![]() 四点共圆,
四点共圆,
∴ ![]() ,
,
∴ ![]() .
.
②当 ![]() 在
在 ![]() 延长线上时,将线段
延长线上时,将线段 ![]() 绕点
绕点 ![]() 逆时针方向旋转
逆时针方向旋转 ![]() 得到线段
得到线段 ![]() ,连接
,连接 ![]() .
.
同理可证: ![]() ,
,
∵ ![]() ,∴四边形
,∴四边形 ![]() .
. ![]() .
. ![]() 、
、 ![]() 四点共圆,∴
四点共圆,∴ ![]() ,
,
∴ ![]() ,
,
综上, ![]() 的度数为
的度数为 ![]() 或
或 ![]() .
.
比值计算如下:
过点 ![]() 作
作 ![]() ,如图,
,如图,
则在 ![]() 中,
中, ![]() ,
, ![]() ,∴
,∴ ![]() ,
, ![]() ,
,
在 ![]() 中,
中, ![]() ,
,
设 ![]() ,
, ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
【解析】(1)利用锐角三角函数的定义及特殊角的三角函数值,即可求出∠B的度数及![]() 的值。
的值。
(2)根据折叠的性质先求出∠FAD、∠EA′G的度数,再利用勾股定理在Rt△A′FD中求出A′F的长,即可得出A′E的长,再利用直角三角形的性质得出A′G的长,然后求出EG的长,从而得到BG的长。
(3)根据题意画出图形,分两种情况讨论:①当 D 在 B C 边上时,将线段 A D 1 绕点 A 顺时针方向旋转 90 ° 得到线段 AE ,连接 BE ,先证明△ABE ≌ △ACD1 ,根据全等三角形的性质及特殊角的三角函数值求出 ∠BD1E=30°,得到四边形 A . D1 、 B . E 四点共圆,然后根据圆周角定理即可求出结果;②当 D 在 B C 延长线上时,将线段 A D 绕点 A 逆时针方向旋转 90 ° 得到线段 A F ,连接 C F .同①的方法类似求出结果即可,根据锐角三角函数的定义得出AD=![]() ,再求出ED的长,然后根据AD=
,再求出ED的长,然后根据AD=![]() x,即可求出结果。
x,即可求出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和
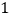 个过滤网要花费
个过滤网要花费 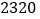 元,买
元,买 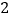 个空气净化器和
个空气净化器和 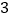 个过滤网要花费
个过滤网要花费 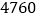 元.
元.
(1)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(2)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买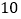 个空气净化器和
个空气净化器和 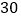 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中,  ,对角线
,对角线  平分
平分  .
.
(1)求证: .
.
(2)若 ,
,  ,
,  ,求
,求  的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道一次函数
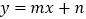 与
与 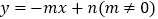 的图象关于
的图象关于 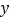 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数 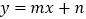 与
与 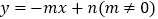 互为“镜子”函数.
互为“镜子”函数.
(1)请直接写出函数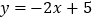 的“镜子”函数
的“镜子”函数
(2)如果一对“镜子”函数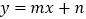 与
与 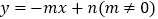 的图象交于点
的图象交于点 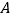 ,且与
,且与 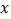 轴交于
轴交于  、
、  两点,如图所示,若
两点,如图所示,若 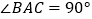 ,且
,且 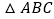 的面积是
的面积是 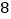 ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.
(3)若点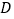 是
是 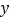 轴上的一个动点,当
轴上的一个动点,当 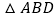 为等腰三角形时,直接写出点
为等腰三角形时,直接写出点 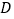 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】据媒体报道,我国因环境污染造成的巨大经济损失,每年高达860 000 000元,这个数用科学记数法表示为元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x
1
2
3
4
水位y(米)
20.00
20.50
21.00
21.50
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的一边
的一边  为平面镜,
为平面镜,  ,在
,在  上有一点
上有一点  ,从
,从  点射出一束光线经
点射出一束光线经  上一点
上一点  反射,反射光线
反射,反射光线  恰好与
恰好与  平行,则
平行,则  的度数是( )
的度数是( )
A.
B.
C.
D.
相关试题

