【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和 ![]() 个过滤网要花费
个过滤网要花费 ![]() 元,买
元,买 ![]() 个空气净化器和
个空气净化器和 ![]() 个过滤网要花费
个过滤网要花费 ![]() 元.
元.
(1)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(2)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买 ![]() 个空气净化器和
个空气净化器和 ![]() 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
参考答案:
【答案】
(1)解:设一个空气净化器 ![]() 元,一个过滤网
元,一个过滤网 ![]() 元,
元,
![]() ,
,
则一个空气净化器 ![]() 元,一个过滤网
元,一个过滤网 ![]() 元
元
(2)解:国美: ![]() (元),
(元),
苏宁:一个净化器送两个过滤网,那么 ![]() 个净化器送
个净化器送 ![]() 个网,只需买
个网,只需买 ![]() 个网即可.
个网即可.
∴ ![]() (元),
(元),
∵ ![]() ,
,
∴苏宁更合算
【解析】(1) 此题的等量关系式是:买一个空气净化器的价钱+1 个过滤网的价钱= 2320 ;买 2 个空气净化器价钱+ 3 个过滤网的价钱= 4760 。设未知数,建立方程组,求解即可。
(2)根据“国美”和“苏宁”的促销活动,分别算出在两家商场购买10 个空气净化器和 30 个过滤网所花费的钱,再比较大小即可得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使
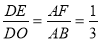 ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当
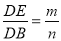 时,请猜想
时,请猜想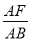 的值(请直接写出结论).
的值(请直接写出结论).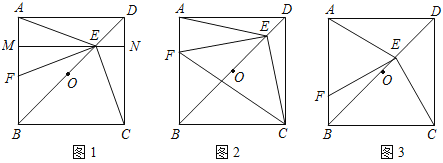
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣4x﹣3向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )
A.y=(x+1)2﹣2
B.y=(x﹣5)2﹣2
C.y=(x﹣5)2﹣12
D.y=(x+1)2﹣12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1,b1为常数,且k1≠0),直线l2:y=k2x+b2(k2,b2为常数,且k2≠0),若l1⊥l2,则k1·k2=-1.
解决问题:
①若直线y=3x-1与直线y=mx+2互相垂直,求m的值;
②是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,
中,  ,对角线
,对角线  平分
平分  .
.
(1)求证: .
.
(2)若 ,
,  ,
,  ,求
,求  的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道一次函数
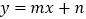 与
与 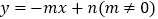 的图象关于
的图象关于 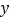 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数 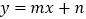 与
与 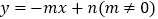 互为“镜子”函数.
互为“镜子”函数.
(1)请直接写出函数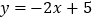 的“镜子”函数
的“镜子”函数
(2)如果一对“镜子”函数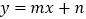 与
与 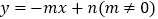 的图象交于点
的图象交于点 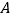 ,且与
,且与 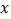 轴交于
轴交于  、
、  两点,如图所示,若
两点,如图所示,若 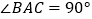 ,且
,且 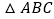 的面积是
的面积是 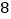 ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.
(3)若点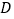 是
是 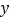 轴上的一个动点,当
轴上的一个动点,当 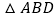 为等腰三角形时,直接写出点
为等腰三角形时,直接写出点  的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)【结论再现】如图①,在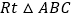 中,
中, 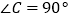 ,
, 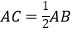 ,则
,则 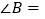
 ,
, 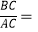 .
. 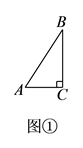
(2)【问题解决】
如图②,四边形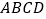 是一张边长为
是一张边长为 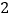 的正方形纸片,
的正方形纸片, 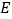 、
、 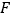 分别为
分别为 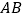 、
、 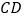 的中点,沿过点
的中点,沿过点 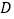 的折痕将纸片翻折,使点
的折痕将纸片翻折,使点 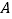 落在
落在 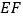 上的点
上的点 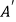 处,折痕交
处,折痕交 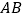 于点
于点 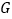 ,求
,求 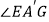 的度数和
的度数和 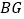 的长.
的长.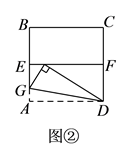
(3)【问题探究】
如图③,点 是等腰
是等腰 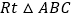 斜边
斜边 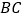 所在直线上一点,且满足
所在直线上一点,且满足 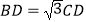 ,求
,求  的大小和此时
的大小和此时 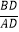 的值.
的值.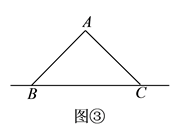
相关试题

