【题目】如图,在四边形 ![]() 中,
中, ![]() ,对角线
,对角线 ![]() 平分
平分 ![]() .
.
(1)求证: ![]() .
.
(2)若 ![]() ,
, ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
参考答案:
【答案】
(1)解:如图,

过 ![]() 点作
点作 ![]() ,
, ![]() ,
,
∵ ![]() 是
是 ![]() 的角平分线,
的角平分线,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]()
![]() ,
,
∴ ![]() ,
,
又∵ ![]() ,
,
∴ ![]() .
.
(2)解:∵ ![]() 且
且 ![]() 和
和 ![]() 为直角三角形,
为直角三角形,
∴设 ![]() ,
,
则 ![]() ,
, ![]() ,
,
而又∵ ![]() ≌
≌ ![]() ,
, ![]() ≌
≌ ![]() ,
,
∴ ![]() ,
,
即 ![]() ,解得
,解得 ![]() ,
,
∴ ![]() ,
,
则 ![]() 的长为
的长为 ![]()
【解析】(1)抓住已知条件AC平分 ∠B AD, 过C点作CE⊥AB , CF⊥AD,可证得CE=CF,再根据BC=CD,就可证明△CFD ≌ △CEB,得出∠D=∠EBC,然后根据∠EBC+∠B=180° ,即可证得结论。
(3)根据已知条件易证△BEC 和 △FDC 为等腰直角三角形,设它们的直角边长为x,就可表示出AE、AF的长,再根据全等三角形的性质证得AE=AF,建立关于x的方程,求出x的值,然后根据勾股定理,在Rt△ACF中就可求出AC的长。
【考点精析】通过灵活运用角平分线的性质定理和勾股定理的概念,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣4x﹣3向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )
A.y=(x+1)2﹣2
B.y=(x﹣5)2﹣2
C.y=(x﹣5)2﹣12
D.y=(x+1)2﹣12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1,b1为常数,且k1≠0),直线l2:y=k2x+b2(k2,b2为常数,且k2≠0),若l1⊥l2,则k1·k2=-1.
解决问题:
①若直线y=3x-1与直线y=mx+2互相垂直,求m的值;
②是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和
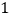 个过滤网要花费
个过滤网要花费 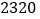 元,买
元,买 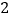 个空气净化器和
个空气净化器和 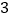 个过滤网要花费
个过滤网要花费 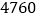 元.
元.
(1)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(2)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买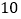 个空气净化器和
个空气净化器和 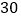 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道一次函数
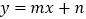 与
与 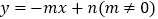 的图象关于
的图象关于 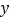 轴对称,所以我们定义:函数
轴对称,所以我们定义:函数 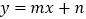 与
与 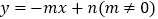 互为“镜子”函数.
互为“镜子”函数.
(1)请直接写出函数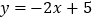 的“镜子”函数
的“镜子”函数
(2)如果一对“镜子”函数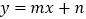 与
与 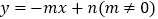 的图象交于点
的图象交于点 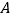 ,且与
,且与 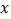 轴交于
轴交于  、
、  两点,如图所示,若
两点,如图所示,若 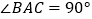 ,且
,且 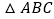 的面积是
的面积是 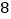 ,求这对“镜子”函数的解析式.
,求这对“镜子”函数的解析式.
(3)若点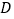 是
是 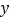 轴上的一个动点,当
轴上的一个动点,当 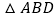 为等腰三角形时,直接写出点
为等腰三角形时,直接写出点 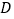 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)【结论再现】如图①,在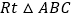 中,
中, 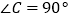 ,
, 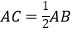 ,则
,则 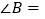
 ,
, 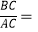 .
. 
(2)【问题解决】
如图②,四边形 是一张边长为
是一张边长为  的正方形纸片,
的正方形纸片, 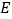 、
、 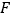 分别为
分别为 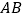 、
、 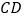 的中点,沿过点
的中点,沿过点 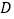 的折痕将纸片翻折,使点
的折痕将纸片翻折,使点 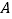 落在
落在 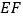 上的点
上的点 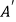 处,折痕交
处,折痕交 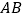 于点
于点 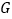 ,求
,求 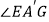 的度数和
的度数和 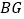 的长.
的长.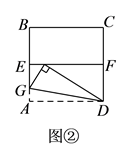
(3)【问题探究】
如图③,点 是等腰
是等腰  斜边
斜边  所在直线上一点,且满足
所在直线上一点,且满足 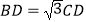 ,求
,求  的大小和此时
的大小和此时 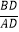 的值.
的值.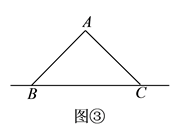
-
科目: 来源: 题型:
查看答案和解析>>【题目】据媒体报道,我国因环境污染造成的巨大经济损失,每年高达860 000 000元,这个数用科学记数法表示为元.
相关试题

