【题目】不等式组 ![]() 的解集在数轴上表示为( )
的解集在数轴上表示为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解: ![]() , 解不等式①得,x≤1,
, 解不等式①得,x≤1,
解不等式②得,x>﹣2,
在数轴上表示如下: ![]()
故选B.
【考点精析】掌握不等式的解集在数轴上的表示和一元一次不等式组的解法是解答本题的根本,需要知道不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
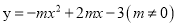 .
.(1)若该二次函数的最小值为-4,求该二次函数解析式;
(2)当
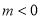 且
且 时,函数值y的取值范围是-6≤y≤5-n,求n的值;
时,函数值y的取值范围是-6≤y≤5-n,求n的值;(3)在(1)的条件下,将此二次函数平移,使平移后的图象经过(1,0).设平移后的图象对应的函数表达式为
 ,当x<2时,y随x的增大而减小,求k的取值范围.
,当x<2时,y随x的增大而减小,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校有一长方形花圃,里面有一些杂草需要处理.小聪单独完成这项杂草清除任务需要150分钟,小聪单独施工30分钟后,小明加入清理,两人又共同工作了15分钟,完成总清理任务的
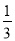 .
.(1)小明单独完成这项清理任务需要多少分钟?
(2)为了加快清理,二人各自提高工作效率,设小明提高后的工作效率是m,小聪提高后的工作效率是小明提高后的工作效率的k倍(1≤k≤2),若两人合作40分钟后完成剩余的杂草清除任务,则m的最大值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】五子连珠棋和象棋、围棋一样,深受广大棋友的喜爱,其规则是:15×15的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上连成五子者为胜.如图是两个五子棋爱好者甲和乙的对弈图(甲执黑子先行,乙执白子后走),观察棋盘思考:若A点的位置记作(8,4),甲必须在哪个位置上落子,才不会让乙在短时间内获胜?为什么?
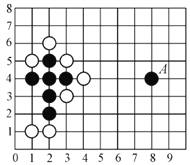
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的面积为40,AD为△ABC的中线,BD=5,BE为△ABD的中线, EF⊥BC,则点E到BC边的距离为( )
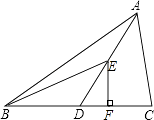
A.2
B.3
C.4
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个三角形有一边上的中线与这边的长相等,那么称这个三角形为“和谐三角形”.
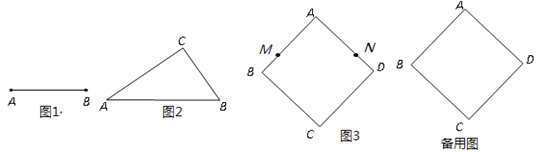
(1)请用直尺和圆规在图1中画一个以线段AB为一边的“和谐三角形”;
(2)如图2,在△ABC中,∠C=90°,AB=
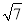 ,BC=
,BC=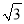 ,请你判断△ABC是否是“和谐三角形”?证明你的结论;
,请你判断△ABC是否是“和谐三角形”?证明你的结论;(3)如图3,已知正方形ABCD的边长为1,动点M,N从点A同时出发,以相同速度分别沿折线AB﹣BC和AD﹣DC向终点C运动,记点M经过的路程为S,当△AMN为“和谐三角形”时,求S的值.
-
科目: 来源: 题型:
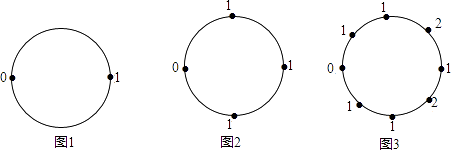
查看答案和解析>>【题目】如图所示,每个圆周上的数是按下述规则逐次标出的:第一次先在圆周上标出0,1两个数(如图1);第二次又在第一次标出的两个数之间的圆周上,分别标出这两个数的和(图2);第三次再在第二次标出的所有相邻两数之间的圆周上,分别标出相邻两数的和(如图3).按此规则以此类推,第2013次标完数字后,圆周上所有数字的和S2013= .
相关试题

