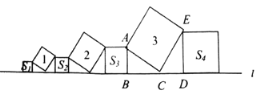
【题目】在直线![]() 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是
上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是![]() ,则
,则![]() _______.
_______.
参考答案:
【答案】2
【解析】
首先通过等角转换,即可得出∠BAC=∠DCE,∠ACB=∠CED,即可判定△ABC≌△CDE,进而得出AB=CD,BC=DE,再利用勾股定理,即可得出![]() ,同理可证,
,同理可证,![]() ,即可得解.
,即可得解.
解:∵在△ABC和△CDE中,
∠BAC+∠BCA=∠ECD+∠CDE=90°,∠ACB+∠ECD=90°
∴∠BAC=∠DCE,∠ACB=∠CED
又∵AC=CE
∴△ABC≌△CDE,
∴AB=CD,BC=DE,
∴AB2+DE2=DE2+CD2=CE2=3,
即为![]() ,
,
同理可证,![]()
∴![]() ,
,
故答案为2.
-
科目: 来源: 题型:
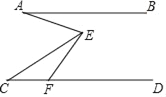
查看答案和解析>>【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写表:
图形序号
①
②
③
④
…
⑩
每个图案中棋子个数
5
8
…
(2)写出第n个“T”字形图案中棋子的个数(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子多少个?
(4)计算前20个“T”字形图案中棋子的总个数.(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
-
科目: 来源: 题型:
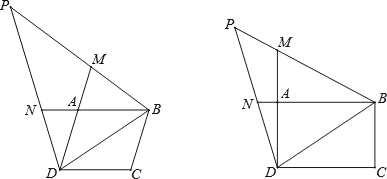
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点M、N分别在线段DA、BA的延长线上,且BD=BN=DM,连接BM、DN并延长交于点P.
(1)求证:∠P=90°﹣
 ∠C;
∠C;(2)当∠C=90°,ND=NP时,判断线段MP与AM的数量关系,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和∠AOE的余角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4
 ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的内容,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0,
∴m2+2mn+n2+n2﹣6n+9=0,
∴(m+n)2+(n﹣3)2=0,
∴m+n=0,n﹣3=0,
∴m=﹣3,n=3
问题:
(1)若x2+2y2+2xy﹣4y+4=0,求
 x+y的值.
x+y的值.(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
相关试题

