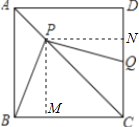
【题目】如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=4![]() ,CQ=10,则正方形ABCD的面积为 .
,CQ=10,则正方形ABCD的面积为 .

参考答案:
【答案】324
【解析】
试题分析:作PM⊥BC于点M,PN⊥CD于点N,利用正方形的性质和角平分线上的点到角的两边相等以及已知条件即可证明△BPM≌△QPN,得出BM=QN,设BM=x,则NF=x,PM=CM=CN=10+x,根据平行线分线段成比例定理即可得到关于x的比例式,求出x的值,即可求出正方形的边长,进而求出其面积.
解:作PM⊥BC于点M,PN⊥CD于点N,如图所示:
∵四边形ABCD是正方形,
∴AC平分∠BCD,
∴PM=PN,∠NEM=90°,
∴四边形PMCN为正方形,∵PQ⊥BP,∴∠BPQ=90°,
∴∠BPM=∠NPQ,
在△BPM和△QPN中,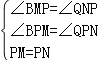 ,
,
∴△BPM≌△QPN(AAS),
∴BM=QN;
设BM=x,则NF=x,
∴PM=CM=CN=10+x,
∴CP=![]() (10+x),
(10+x),
∵PM∥AB,
∴![]() ,即
,即![]() ,
,
解得:x=4或x=﹣10(舍),
∴BM=4,CM=14,
∴BC=BM+CM=18,
∴正方形ABCD的面积为:18×18=324.
故答案为:324.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句正确的是( )
A.画直线AB=10厘米
B.画直线l的垂直平分线
C.画射线OB=3厘米
D.延长线段AB到点C,使得BC=AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度运动,连接AD、AE,设运动时间为t秒.
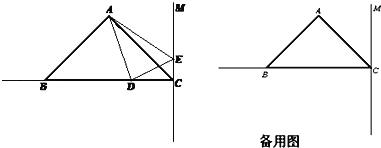
(1)求AB的长;
(2)当t为多少时,△ABD的面积为6cm2?
(3)当t为多少时,△ABD≌△ACE,并简要说明理由.(可在备用图中画出具体图形)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB和△ACD是等边三角形,O、A、C在x轴上,B、D在y=
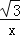 (x>0)的图象上,则点C的坐标是( )
(x>0)的图象上,则点C的坐标是( )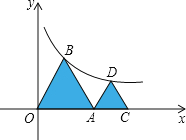
A.(﹣1+
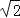 ,0) B.(1+
,0) B.(1+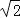 ,0) C.(2
,0) C.(2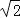 ,0) D.(2+
,0) D.(2+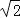 ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a3﹣25a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四种说法:①线段AB是点A与点B之间的距离;②射线AB与射线BA表示同一条射线;③两点确定一条直线;④两点之间线段最短.其中正确的个数是 ( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3x2y的系数是__________;
相关试题

