【题目】如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=70°,求∠DOE和∠EOF的度数;
(2)请写出图中∠AOD的补角和∠AOE的余角.

参考答案:
【答案】(1) 90°;(2)∠AOD的补角:∠AOC和∠BOD;∠AOE的余角:∠DOF和∠BOF.
【解析】
(1)根据邻补角的定义求出∠AOD,再根据角平分线的定义求解即可得到∠DOE,根据对顶角相等可得∠BOD=∠AOC,再根据角平分线的定义∠DOF,然后根据∠EOF=∠DOE+∠DOF计算即可得解;
(2)根据邻补角的定义和互补的角的定义解答即可;根据互余的角的定义解答即可.
(1)因为∠AOC=70°,
所以∠AOD=180°-∠AOC=110°,
所以∠BOD=180°-∠AOD=70°.
又因为OE平分∠AOD,所以∠DOE=![]() ∠AOD=55°,
∠AOD=55°,
又因为OF平分∠BOD,所以∠DOF=![]() ∠BOD=35°.
∠BOD=35°.
所以∠EOF=∠DOE+∠DOF=90°.
(2)∠AOD的补角:∠AOC和∠BOD;
∠AOE的余角:∠DOF和∠BOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:
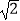 ≈1.41,
≈1.41, 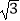 ≈1.73)
≈1.73) 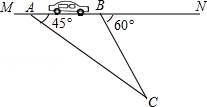
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB.
(1)用没有刻度的直尺和圆规按所给的要求作图:点C在线段BA的延长线上,且CA=AB;
(2)在(1)中,如果AB=28 cm,线段BC上有一点M,且线段AM∶BM=1∶3,求线段CM的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
-
科目: 来源: 题型:
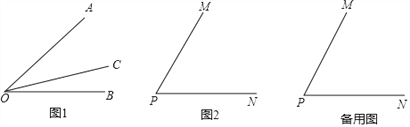
查看答案和解析>>【题目】【探索新知】:如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示出所有可能的结果)
【深入研究】:如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.
(3)当t为何值时,射线PM是∠QPN的“巧分线”;
(4)若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请直接写出当射线PQ是∠MPN的“巧分线”时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件. ①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.

(1)求证:DE是⊙O的切线;
(2)如果AD=5,AE=4,求AC长.
相关试题

