【题目】如图,在△ABC中,∠B=90°,tan∠C= ![]() ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2
参考答案:
【答案】C
【解析】解:∵tan∠C= ![]() ,AB=6cm,
,AB=6cm,
∴ ![]() =
= ![]() ,
,
∴BC=8,
由题意得:AP=t,BP=6﹣t,BQ=2t,
设△PBQ的面积为S,
则S= ![]() ×BP×BQ=
×BP×BQ= ![]() ×2t×(6﹣t),
×2t×(6﹣t),
S=﹣t2+6t=﹣(t2﹣6t+9﹣9)=﹣(t﹣3)2+9,
P:0≤t≤6,Q:0≤t≤4,
∴当t=3时,S有最大值为9,
即当t=3时,△PBQ的最大面积为9cm2;
故答案为:C.
根据解直角三角形中正切的定义,求出BC的值,由三角形的面积公式得到二次函数,由顶点式得到最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的直径,
的直径, 是
是 的切线,
的切线, 是切点,
是切点,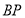 与
与 交于点
交于点 .
.
(1)如图①,若
 ,
, ,求
,求 的长;
的长;(2)如图②,若
 为
为 的中点,求证:直线
的中点,求证:直线 是
是 的切线.
的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】为美化市容市貌,我市在春节前夕计划在市区几个公园建造
 、
、 两种型号花灯供市民观赏,根据预算,共需资金
两种型号花灯供市民观赏,根据预算,共需资金 万元.若建造一个
万元.若建造一个 种花灯和两个
种花灯和两个 类种花灯共 需资金
类种花灯共 需资金 万元;建造两个
万元;建造两个 种花灯和一个
种花灯和一个 种花灯共需资金
种花灯共需资金 万元.
万元. (1)问建造一个
 种型号花灯和一个
种型号花灯和一个 种型号花灯所需资金分别是多少万元?
种型号花灯所需资金分别是多少万元? (2)若建造
 种型号花灯不超过
种型号花灯不超过 个,则
个,则 种型号花灯至少要建造多少个?
种型号花灯至少要建造多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
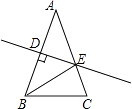
A.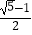
B.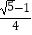
C.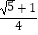
D.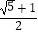
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下题和解题过程:化简
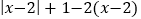 ,使结果不含绝对值.
,使结果不含绝对值.解:当
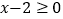 时,即
时,即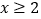 时,
时, 原式

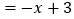 ;
;当
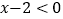 ,即
,即 时,
时,原式
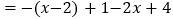
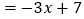
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:
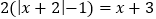 ;
;(2)试探究:当
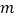 分别为何值时,方程
分别为何值时,方程
①无解,②只有一个解,③有两个解
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).

(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
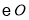 的直径
的直径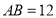 ,
,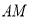 ,
,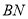 是
是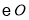 的两条切线,
的两条切线,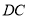 切
切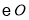 于
于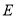 ,交
,交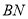 于
于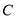 ,设
,设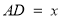 ,
,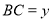 ,
, .
.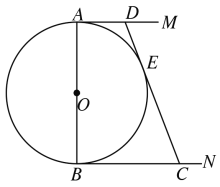
(1)求
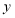 与
与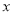 的函数关系式;
的函数关系式;(2)若
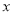 ,
,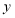 是
是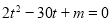 的两实根,求
的两实根,求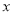 ,
,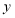 的值;
的值;(3)在(2)的前提下,求
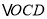 的面积.
的面积.
相关试题

