【题目】如图,![]() 的直径
的直径![]() ,
,![]() ,
,![]() 是
是![]() 的两条切线,
的两条切线,![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
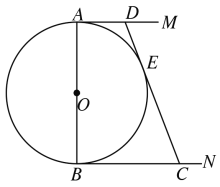
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若![]() ,
,![]() 是
是![]() 的两实根,求
的两实根,求![]() ,
,![]() 的值;
的值;
(3)在(2)的前提下,求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)45
;(3)45
【解析】
(1)作DF⊥BN交BC于F;根据切线长定理得到BF=AD=x,CE=CB=y,则DC=DE+CE=x+y,在直角△DFC中根据勾股定理,就可以求出y与x的关系;
(2)由(1)求得xy=36,然后由根与系数的关系求得a的值,通过解一元二次方程即可求得x、y的值;
(3)由AM,BN是圆 O的两条切线,DC切圆 O于E,得到OE⊥CD,AD=DE,BC=CE,利用三角形面积公式即可求解.
(1)如图,作DF⊥BN交BC于F;
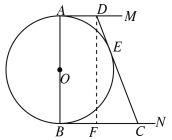
∵AM、BN与O切于点A、 B,
∴AB⊥AM,AB⊥BN.
又∵DF⊥BN,
∴∠BAD=∠ABC=∠BFD=90°,
∴四边形ABFD是矩形,
∴BF=AD=x,DF=AB=12,
∵BC=y,
∴FC=BCBF=yx;
∵DE切O于E,
∴DE=DA=x,CE=CB=y,
则DC=DE+CE=x+y,
在Rt△DFC中,
由勾股定理得:(x+y)2=(yx)2+122,
整理为:![]() ,
,
∴y与x的函数关系式是![]() .
.
(2)由(1)知xy=36,
x,y是方程2t230t+a=0的两个根,
∴根据韦达定理知,xy=![]() ,即a=72;
,即a=72;
∴原方程为t215t+36=0,
解得![]() 或
或![]()
∵x<y,
∴![]() ;
;
(3)如图,连接OD,OE,OC,
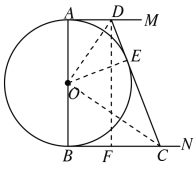
∵AD,BC,CD是圆O的切线,
∴OE⊥CD,AD=DE=3,BC=CE=12,
∴S△COD=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,tan∠C=
 ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下题和解题过程:化简
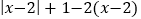 ,使结果不含绝对值.
,使结果不含绝对值.解:当
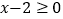 时,即
时,即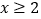 时,
时, 原式

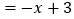 ;
;当
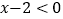 ,即
,即 时,
时,原式
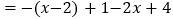
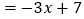
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:
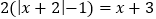 ;
;(2)试探究:当
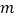 分别为何值时,方程
分别为何值时,方程
①无解,②只有一个解,③有两个解
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).

(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(2,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(a,b),且a=
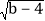 +
+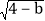 -6
-6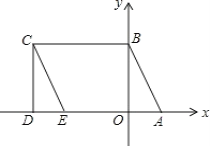
(1)求点C的坐标;
(2)求点E的坐标;
(3)点P是CE上一动点,设∠CBP=x°,∠PAD=y°,∠BPA=z°,确定x,y,z之间的数量c关系,并证明你的结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=12,AC=
 ,∠B=30°,则△ABC的面积是 .
,∠B=30°,则△ABC的面积是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
相关试题

