【题目】如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( ) 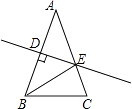
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:∵△ABC中,AB=AC=4,∠C=72°, ∴∠ABC=∠C=72°,∠A=36°,
∵D是AB中点,DE⊥AB,
∴AE=BE,
∴∠ABE=∠A=36°,
∴∠EBC=∠ABC﹣∠ABE=36°,
∠BEC=180°﹣∠EBC﹣∠C=72°,
∴∠BEC=∠C=72°,
∴BE=BC,
∴AE=BE=BC.
设AE=x,则BE=BC=x,EC=4﹣x.
在△BCE与△ABC中,![]() ,
,
∴△BCE∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得x=﹣2±2 ![]() (负值舍去),
(负值舍去),
∴AE=﹣2+2 ![]() .
.
在△ADE中,∵∠ADE=90°,
∴cosA= ![]() =
= ![]() =
= ![]() .
.
故选C.
【考点精析】通过灵活运用解直角三角形,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的直径,
的直径, 是
是 的切线,
的切线, 是切点,
是切点,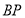 与
与 交于点
交于点 .
.
(1)如图①,若
 ,
, ,求
,求 的长;
的长;(2)如图②,若
 为
为 的中点,求证:直线
的中点,求证:直线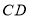 是
是 的切线.
的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】为美化市容市貌,我市在春节前夕计划在市区几个公园建造
 、
、 两种型号花灯供市民观赏,根据预算,共需资金
两种型号花灯供市民观赏,根据预算,共需资金 万元.若建造一个
万元.若建造一个 种花灯和两个
种花灯和两个 类种花灯共 需资金
类种花灯共 需资金 万元;建造两个
万元;建造两个 种花灯和一个
种花灯和一个 种花灯共需资金
种花灯共需资金 万元.
万元. (1)问建造一个
 种型号花灯和一个
种型号花灯和一个 种型号花灯所需资金分别是多少万元?
种型号花灯所需资金分别是多少万元? (2)若建造
 种型号花灯不超过
种型号花灯不超过 个,则
个,则 种型号花灯至少要建造多少个?
种型号花灯至少要建造多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,tan∠C=
 ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A.18cm2
B.12cm2
C.9cm2
D.3cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下题和解题过程:化简
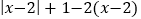 ,使结果不含绝对值.
,使结果不含绝对值.解:当
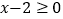 时,即
时,即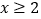 时,
时, 原式

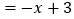 ;
;当
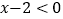 ,即
,即 时,
时,原式
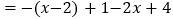
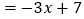
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:
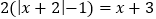 ;
;(2)试探究:当
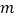 分别为何值时,方程
分别为何值时,方程
①无解,②只有一个解,③有两个解
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).

(1)画出△ABC,并求△ABC的面积.
(2)在平面直角坐标系中平移△ABC,使点C经过平移后的对应点为C'(5,4),平移后△ABC得到△A'B'C',画出平移后的△A'B'C',并写出点A',B'的坐标
(3)P(-3,m)为△ABC中一点,将点P向右平移4个单位后,再向上平移6个单位得到点Q(n,-3),则m= n=
相关试题

